電場と電位
Mathematica を利用した物理 -2-
H.Yanase
このシリーズはMathematicaを利用すると自分で変更し、試行錯誤できるようになっているがMathematicaがなくても理解できるように作成されている。対象は電磁気を学習している高校生がメインである。あくまで電場と電位を理解することが中心なのでMathematicaのプログラムに興味がない読者はプログラム部分はとばして結果だけを見ればよい。Mathematicaの入力は【Mathematicaの入力】で区別してある。Mathematicaがインストールされていれば全てのコマンドは修正、実行が可能であるが理解に必要な結果はCDF(WolframのHPから無償ダウンロード可能)をインストールすればMathematicaがなくてもWebページからも実行できる。これを【実行可能】で表す。(PCの環境によってはプログラムロード、実行に多少時間がかかる場合があります。)
Qとあるのは考えてほしい問題なので、まず、自分の頭と手のみで考えてみてほしい。
Mathematicaを利用する場合は事前にMathematicaの基礎(本HPからダウンロード可能)を読んでおくとよい。
本章ではMathematicaVer8から機能強化されたマウスなどによるダイレクトな入力方法の学習もできるようにしてある。
より細かなプログラムの説明はMathematicaのHPにチュートリアルとして豊富なコンテンツがあるので参考にするとよい。
Mathematica HP:http://www.wolfram.com/
筆者HP：http://www.ne.jp/asahi/buturiwa/ai/EducationM1.htm
１．単一電荷の電場と電位
原点に＋の点電荷がある時、位置ｒでの電位と電場を考えよう。
高校では次のように習った。クーロンの法則から電荷Q1とQ2が距離ｒだけ離れている時の力は
クーロン定数をｋとして
であった。しかし、この式は力を表しているのでベクトルだが左辺は大きさを表すので本来はこれに力の向きを表す単位ベクトルがかかる。その向きは点電荷の位置と符号で決まる。一方で物理学では位置エネルギーUと力Fは山とそれに向かう時の傾きのように次のような関係があった。
微分表記が使えるなら
である。例えばバネの弾性エネルギー 
とすると
が得られる。これはF=ｑEとU=qV を利用するとそのまま電場と電位の関係になる。位置をｒとして
一方でクーロンの法則から 
とし、 
を原点におき、 
を試験電荷として位置rで観測すると
と表すことを高校で学習した。しかし、これらの式は正しくない。
1次元の正の値に限っての話であれば問題はないが、その他では問題が出てくる。
最後の電位の式はV=kq/r なのでこれはグラフにした時、rが負になればVも負になってしまうので位置エネルギーを表す山の形にならない。
問題はベクトルとスカラーの関係にある。ベクトル量はベクトル量で、スカラー量はスカラー量で足し引きしないといけない。
しかし、電場 E はベクトルで電位Vはスカラーである。今後 ベクトルは太字、スカラーは普通字で表現することもある。
このベクトルとスカラーの問題は後に発展で扱う。
Q1.下図のように原点に+q[c]の電荷がある場合、距離ｒだけ離れた位置の電場と電位がどうなるか正しく表す式を求めよ。
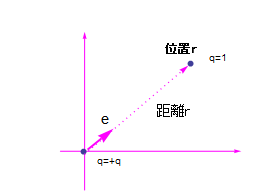
【図1-1】
eは単位ベクトルで e=
のように、あるベクトルをそのベクトルの大きさで割ればいい。向きのみを表す。
正しい電場と電位の式はクーロン点数をｋとして次のようになる。
このように、絶対値を用いるか、場合わけをするか、 
のようにノルム(Norm)、成分を用いた大きさの表現を使うか、をしないといけない。
ただ、物理的には原点に+q[C]の電荷があり、これが他のに対して、力を与える元であるので、ここを山の頂上としたような位置エネルギーがあると考える。
これを正しく式で表現しておくと、電気の位置エネルギーは+,-があり電位と呼んだ。力学の位置エネルギーUと力Fの関係が
で表されたように電位Vと電場Eの関係は
この2つの式は電場と電位の式
で結びつく。これから原点に電荷+qがある時の電場と電位を実際にグラフにしてみよう。
Q2.位置ベクトルrに絶対値をつけておく必要がある。次にこれをグラフにしてみよう。はじめにr＝xの1次元としてE-x,V-xグラフを描いてみよ。
まず、自分の手でグラフを作成し、次にMathematicaを使ってみよう。
【Mathematica入力】
Mathematicaでは絶対値はAbs[ ]というコマンドがあるがここではノルム(大きさ)を求める関数Norm[ ]を利用する。
これは複素数や微積分に対応するので便利だ。以下クーロン定数はk=1で扱う。
Mathematicaのコマンドの詳細はカーソルをコマンドに合わせててF1キーを押すとヘルプが立ち上がり詳細な説明や例が示される。
さらに参照先があるので詳しく調べることもできて数学の基礎勉強にもなる。
まずNorm関数が次のように3平方の定理と絶対値を表していることを確認する。
【Mathematica入力】
原点にqがある時、位置ｒでの電場ｆEと電位fVのグラフを描かせる。fをxでｆを微分させるにはD[ f,x]を使う。
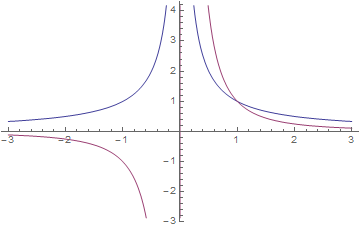
図の青線が電位で赤線が電場である。電場の方が1/2乗という形になっているので傾きが急になることをみておこう。
電位は山（谷）で電場はその傾きにマイナスをかけた形になっている。
この山型のところに負の領域から試験電荷＋１Cが原点に近づくと原点に近くなるほど負方向の力が大きくなる。
また正の方向から原点に近づくと正の負方向の力が大きくなる。
山が電位でその傾きにマイナスをつけると電場、実際に試験電荷の運動経路が電気力線を表す
というイメージはおおざっぱに正しく、重要である。上のグラフを色々変化させて確認しておこう。
しかし、この山に頂上はない。電場の式は分母に距離ｒが入っているので仮に原点に達したとすると∞の力を受けることになるが、現実はそうではない。
原点は特別な位置で未だ習っていない物理が必要になると考えておこう。非常に小さい領域の物理はとてもおもしろいことがいっぱいつまっている。
では同じグラフを電位のrを大きさをとることなく、そのまま描いたらどうなるか、まず自分で描いてみよう。
結果は次のようになる。
【Mathematica入力】Normをとらない場合 図の青線が電位で赤線が電場である。
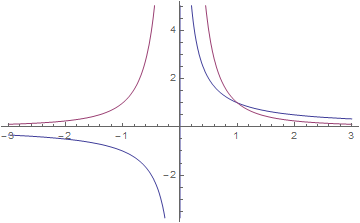
予想通り、Vが双曲線なので山のような形にならず逆にEが急な傾きの山になっている。
このようにクーロン力による電場、電位を考える場合は電位がスカラーで電場がベクトルであることを意識しないといけない。
大学入試問題においてもここがカギになる。また、計算上はスカラーである電位の方がとても扱いやすいことを知っておこう。
実際に4式は単位ベクトルが 
=
/|r| とあらわすことができるから
と3次式と絶対値が出てくる表現が正しい。これを絶対値を使わないで正しく表現することを考えると実に面白いことがある。
後に、この話題に触れることにしよう。
次に立体的なイメージをつかむ。先と同じ原点に１つの+qがあり、任意の位置ｒ(x,y)での電位Vと電場Eはどうなるか考えてみる。
まず電位を表す3次元のグラフを描こう。このあたりはMathematicaがあると便利である。
【Mathematica入力】
電荷の大きさを変数にとり、任意に変更し、実行できるようにManipulate[]を利用しよう。高さの最大は10にしてある。
Manipulate[]を使うと簡単にマウスから動かしてその変化をすぐに見ることができる。
Mathematicaが自動で判断するので便利だが同じ記号を使用していると混乱が生じる。
そこで以下では時々同じVをVmやV5みたいに区別するが実際は同じ電圧Vと考えてよい。
【実行可能1】
立体図形はマウスでドラッグすればいろいろな角度から確認できる。
また、電荷を＋、-いかに変化させても原点は特別で∞になることを確認しておこう。
この山(谷）の形から電位さらにこの山(谷)の傾きに-をかけると電場が出る。これがルールだった。
Q3.次に2次元の場合、電位Vを電荷qが位置(a,b)にある時として、電位Vと電場Eのx、y成分を求めよ。
さらにそのグラフを描いてみよ。まず、自分の手でやってみることだ。
これなら分母が負になることはない。Norm関数を使わない表記だ。
電位Vはスカラーだが電場はベクトルなので次の関係を用いて成分に分ける。
これは2式から次のように微分ができれば簡単に求まる。
ではこれに従ってまず、自分で上のVから電場Eのｘ成分とｙ成分を求めてみよう。
電荷1が原点にあるとして電位をxで微分したものを電場Ex、yで微分したものをEyとして微積を学習しているならば自分で計算してみること。
Mathematicaを使うと次のように簡単に結果を確認できる。
【Mathematica入力】x=a,y=bに電荷がある時の電場を求める。
正しく求まっただろうか。 
を先にXで微分し、後でXの微分をかけ、 ｘで微分するときはｙは定数のように扱えばよい。
このルートの微分はよく登場するので何度も練習して身につけておこう。
これでx、ｙ成分のExとEyが得られたのでこれをグラフにしてみよう。
x成分もy成分も座標ｘ、ｙの関数なのでそれぞれを3次元のグラフにしてみよう。
まず、自力で電位、電場のイメージを描けただろうか？
【Mathematica入力】点電荷が原点にある時の電位と電場のｘ、y成分を表示させる。
【実行可能2】
電場をクリックしてみよう。これははじめに示した。点電荷による電場のグラフだ、ExとEyがちょうど90°回転している関係になっているのがわかる。
しかし、電場はベクトルなのでEx,Eyを眺めてみても全体の様子はつかみにくい。かといって 
で大きさにしてしまうと電位のグラフとさほどかわらなくなる。電場を連続していけば電気力線になった。そこで次に電気力線で電場を表すことをしてみよう。
Q4 次に電位のグラフを+Z方向、上から眺めた時の電気力線の様子を図に表せ。また、等電位面も図示せよ。
Mathematicaには等高線を表す専門の関数ContourPlotが用意されていて、これを用いると、電場や電位は簡単に示すことができる。
Ex,Eyをベクトルの成分としてこれを結んだ線で電気力線になった。。Mathematicaには便利なStremPlotという関数があるのでこれを利用しよう。
【Mathematica入力】 StreamPlot 流線を表示させる。先に定義したＶを利用する。ただしｋ＝１とする。
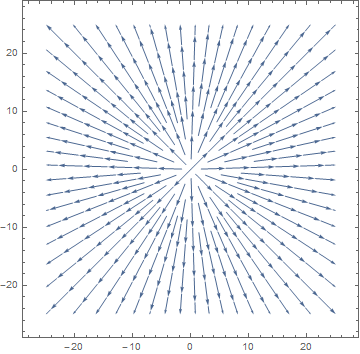
同じようなグラフが描けただろうか。矢印には湧き出し点があり、これは山の頂点で、実際のグラフでは無限に発散している場所だ。
物理学ではこういう点に何か「意味」がある。それを嗅ぎ出せば新しい発見が生まれる。さらに地図でいうと等高線が等電位面である。
これはただ、等間隔の同心円に書いたら間違いである。電気力線の密度が電場の大きさを表したから、中心に近いほど電位の傾きは急になる。
つまり、等電位面の間隔は中心ほど狭くならないといけない。
【Mathematica入力】
同じ電位を用いて等高線を描かせる。(中心付近はカットされている。)
ContourPlotを用いて等電位面を濃淡付きで描かせる。
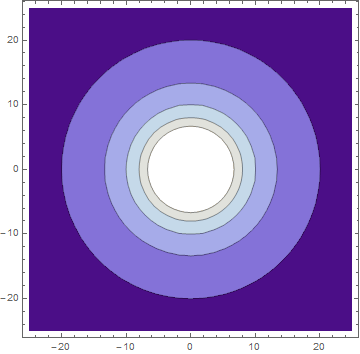
先の等電位線と一緒に表すと電気力線が常に等電位面に直交していることがわかる。これも電気力線の重要な性質だ。
【Mathematica入力】 Show[ ]は複数のグラフを合わせて表示させる。ContourShading→Noneのオプションをつけると濃淡の色をつけない。
【実行可能3】
この平面図からはじめに見た立体図が想像できるだろうか。等電位面等高線である等高線のこみ具合から中心に近づくほど急に高くなることがわかる。
次に応用して2つの電荷がある場合について考えよう。電気力線の密度は電場の強さそのものになった。
しかし、上のプログラムはそこまでは正確に表現していない。電気力線を考えたのはファラデーである。
この流線によって鮮やかに電場のイメージを表現できるようになった。
この流線、流れの表現は電場のように目にみえない力がどう働いているかを見ることができる。
これはベクトル場と呼ばれ、現在でもベクトル場として先端分野でも応用される。
この節の最後にいくつかの単純なベクトル場をMathematicaで紹介しておこう。場というものを理解する手助けになればいい。
【Mathematica入力】それぞれの成分が座標に比例する場合のベクトル場
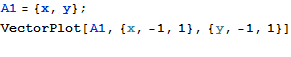
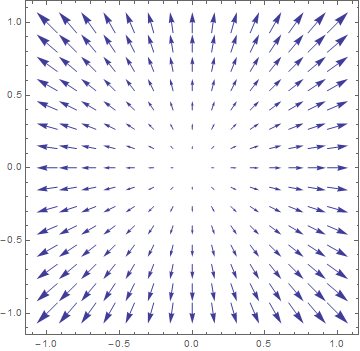
【Mathematica入力】
x成分がy座標に、y成分が-ｘ座標に比例する場合のベクトル場、これは回転を表している。
行列式の公式を思い浮かべると「あっ」と思うのではないかな。
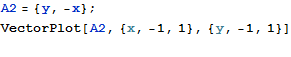
２．複数電荷の電場と電位
では次に2つの電荷が距離ｄだけ離れている場合について見ていこう。
x=-d/2の位置に点電荷q1,x=d/2の位置にq2の電荷を置く。
Q6.点Pでの電場と電位を求める式をつくり、そのグラフを表せ。
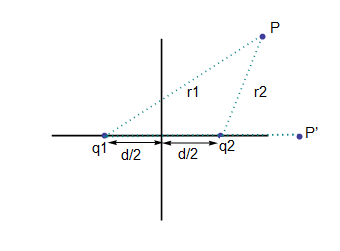
【図2-1】
この時、まずｘ軸上の点P’での電位Vと電場Eはどなるか考えてみよう。式(4)のクーロンの法則から
ｘ軸上の位置xに試験電荷＋１Ｃを持ってくれば
これに働く力が電場になるのでq1からは単純にクーロンの法則から
q2からは
となる。よって両方からの影響はこれらを足せばいいが、ここに注意がいる。
まず電位Vはスカラーなので単純に次のようにたしてもよい。
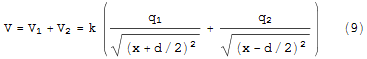
ところが電場はベクトルなので成分で考えて足し合わせをしないといけない。
ここではｘ軸上で考えているので先に求めたE1,E2はｘ成分となるが力の向きを正しく表していない。
q1,q2が＋の電荷だとするとP’の位置が両電荷の内にある場合と外にある場合で向きが変化するはずだ。
しかし3式からは次のように合成された電場Ｅはｘがいくつであっても正の値になってしまう。
そこで5式から正しくは次のようにかかないといけない。
クーロンの法則に頼らず、微分を用いれば、(9)式から直接
+
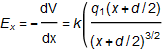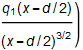
が得られる。電位がスカラーで電場がベクトルなので、この場合はxで微分し、電場のx成分が求まる。
2次元の場合は同様にyで微分し、y成分も求めればよい。
ではこのグラフを具体的に書いてみよう。特にxが-d<x<dの時とそうでない時で注意し、まず自分で描いてみること。
【Mathematica入力】 図の青線が電位で橙線が電場である。実際にMathematicaがある人は最後を
にかえて正しくならないことを確認してみるといい。
【実行可能4】
電荷１，２を同じを＋か-に合わせると、どんな電荷でも電位は原点をとおらないで電場は原点を通る。
これは電位が山（谷）なので同じ山（谷）の中点は平らにはなるが高さ、深さは0にならない。つまり傾きである電場は0になり、電位は０にならない。
また、電荷１，２を異なる正負で同じ値にすると原点では逆に電位が0になり、電場は0になることを確認しておこう。
電荷1を+2にし、電荷2を-１に固定する。電荷1を大きくしていくと電荷2の右側の領域で電場のグラフがｘ軸を横切ることも確認しよう。
この時、グラフでｘ軸を横切る点は1つだけになる。しかし、単純に電場の公式からE=0となるｘの値を求めようとすると2次方程式になり、解が2つ出てくる場合があるが、どちらかの解は不適である場合があるので注意しよう。その確認の意味でも常に電場の向きは＋１Cの試験電荷を持って来て正を向くか負を向くかで判断できるようにしておこう。
もう一つこのグラフを利用してみみておいてほしいことがある。電荷1を0.5、電荷2を-2、電荷の間隔を0.5にしてみると、下図のようなグラフが描ける。
どんな電場や電位も電荷のある場所から遠く離れれば0になることはわかるだろう。でもこの時、電荷1の右側(x軸の負方向)に電場がx軸を横切る場所が
現れる。つまり、x軸上でこの位置に電荷をおいても動かないわけだ。電荷の大きさに差がないとこのような位置はx軸上に現れない。
電荷の差がなくなるにつれて、この位置はx軸の遠方に追いやられることをみておこう。
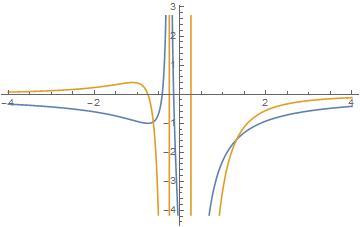
Q7.このグラフにおいて、電荷1を0.5、電荷2を-2、電荷の間隔を0.5の時、電場Eがx軸上で0になる位置を求めよ。
まず、自分で計算してみること。(10)式において2d=0.5 q1=0.5 q2=-2を代入してEx=0をxについて解けばいい。
次の例ではMathematicaでこの計算を実行する手順を示す。
【Mathematica入力】
=0の等式では共通因数のkは省略されるで、先に定義した関数を用いてSolveといコマンドを使うと次のようにx=-0.75という解を得られる。
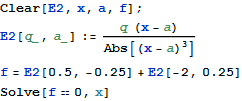
2つの電荷がある時、それがどんな値をとっても上図のような電場Eと電位Vのグラフがかけ、式も扱えるようになっただろうか？
次に2つの電荷の電気力線と等電位面を描く。まずは1つの電荷と同様にして次のように平面図を描かせる。大学入試でもしばしば登場するグラフだ。
この図と式、グラフが自由自在となればまず、電場の基礎はできたことになる。
【Mathematica入力】 チェックをいれると等電位面が描画される。
【実行可能5】
どこでも電気力線と等電位面が直交し、電位のグラフの傾きが大きいところで等電位面は密になっていることが確認できただろうか。
ここでも先と同じように電荷1を0.5、電荷2を-2、電荷の間隔を0.5にしてみると、下図のようなグラフが描ける。
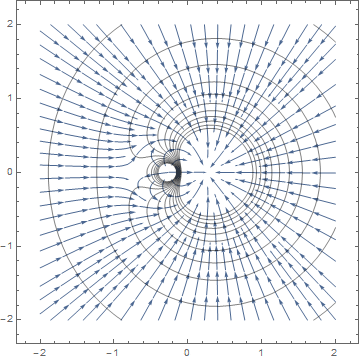
電気力線と等電位面のグラフでもE=0となるx=-0.75の付近が特別だということがわかるだろう。でもV=0となるところはどうだろう。
あくまで電位は高さだからどこでも基準を0にすることができる。具体的にはアースするところが0Vである。何か特別なものを見出せるだろうか。
考えてみておいてほしい。にこの話題に触れる。
次に3次元の様子を描かせる。電位が山（谷）で電場が-（傾き）となることをMathematicaで直接たしかめて欲しい。
マウスでドラッグすると様々な角度で確認できるのでその様子をイメージできるようにしておこう。
さらに次のプログラムでは電位の範囲を選ぶとその値以下の電位については描画がカットされる。すると等電位面の形が確認しやすい。
このオプションを使って等電位面の形も確認して欲しい。
【Mathematica入力】 AspectRatio→1は図形の縦横比を1にする命令である。Mathematicaは通常横長で作図する。
この図は円であることを視覚的に見たいので指定する。分母が0になるとエラーが出るため微少値kで補正する処理を入れた。
パソコンで処理するための特別な操作で式が複雑になる弊害がある。MathematicaにはRegionPlotという領域を指定し、描画する関数もある。
【実行可能6】
いろいろ試したら電位の範囲を１，電荷の距離を１、電荷１を-３，電荷２を１０にセットしてみて欲しい。
そして3次元図から平面図に切り替えると左側の等電位面は卵型のようにゆがむ、しかし電位の範囲を0に変えるとどうなるか？
やってみる前に考えて欲しい。結果はきれいな円ができる。
この状態で電荷2を変化させてもやはりきれいな円が確認できる。実はこの内容は複数の大学の入試のネタになっている。では解いてもらおう。
Q8.前問のようにx軸上に距離d離れて、電荷q1、q2がある時、等電位面が0Vなる面は円であることを示し、その円の方程式を表せ。
まず、自分の手で計算をすすめる。電位が0のになる位置を探ると9式から任意の観測点P(x,y)では
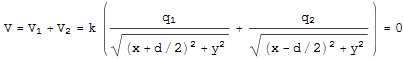
となる。移項して2乗すれば
ここで次のように置き換えると
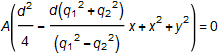
となるのでｋに無関係であることがわかる。さらに
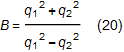
とおくと
を得る。みごとこれは中心が(dB/2,0)円の方程式そのものだ。Bは式(20)から電荷の符号に無関係であることがわかる。
の時は例外としなくてはいけない。
実はこのプログラムには3番目のグラフとして電位0の円を選ぶと式(21)に従った円を太い赤線で描くようになっている。
電荷を変えても見事に円形の等電位面ができることを確認しよう。大きさが等しい電荷を選ぶと円ができない。
これを確かめるために少しづつ、電荷の値を近づけると赤い円の半径はどんどん広がる。そして同じ大きさの電荷になると無限大になる。
円は直線になるわけだ。そのつながりには別の理論がいる。しかし、電磁気の奥深さを実感できるだろう。まだ、磁場は登場していないが。。
さらに電気力線は常に電場に直交し、電荷の運動の経路になっているとを押さえておこう。次の節ではこの電気力線について考える。
３．電気力線
はじめて場という考えに触れる者にとって電場をイメージさせるのが電気力線である。
高校の授業で学んだように+1Cの試験電荷をもってくれば電気力線の方向に電場と等しい力を受け、運動していこうとする。
電位力線は、傾き、強さ、電場をイメージさせる。
一方、高さ、エネルギー、電位をイメージさせるのは等電位面になる。この直交する両者を描くことで場をイメージできるようになる。
電気力線は電場の様子を表している。電気力線の密度が電場Ｅの強さ、線の向きは電場の向きを表した。
電気力線は＋の電荷から出て-の電荷に入る線で、常に空間に一様に広がろうとする性質がある。
現実にこの空間に電荷があれば電気力線が湧き出す口と電気力線を吸い込む口があるわけである。
ファラデーが考えたこのアイディアは目に見えない電場のイメージを鮮やかに表現した。
現代の先端分野でも非常に重要なポイントになる電気力線についてここでもう少し探求する。
電気力線の数Ｎは真空中ではクーロン定数を k として次のように真空中で電荷Qと直接対応している。
N = 4 π kQ
これはさらに真空の誘電率を 
として
【図3-1】
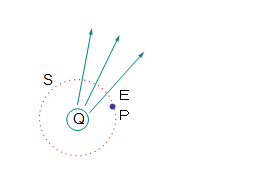
と表すことができた。これは上の図のように電荷から距離ｒの位置Ｐの電場Ｅについては
電荷Ｑから出る電気力線をこの電気力線に垂直な曲面で全ての電気力線を覆う面積をＳとすると
次のガウスの法則が成り立つ。
これは湧き出ている流線を全部ふろしきで包み込めば元の電荷量になるという単純なルールだ。
例えば上の図のように点電荷Ｑから距離ｒの位置でのＥはこの場合の面積 
だから
これと3式と比べれば
が導ける。これから真空には誘電率があり、電気力線は電荷量をこの誘電率で割ったもの 
が1本の線に対応していることになる。
実際の真空の誘電率は 
= 
F/m という値を取る。
これからすると真空が分極しているのかという疑問が湧くかもしれない。しかし、真空はとりあえず分極はしない。(としておく!）
従って真空中では光や電磁波の伝達速度は一定で 3.0×10
m/s は変化しない。変化しないどころか、
どんな速さの乗り物から見ても一定になる重要な数値だ。この光の速さに真空の誘電率は 
は関係している。
相棒である磁場を伝える透磁率を学ぶと光速はこの2つの量で完全に決まる！
この話は次回に詳しくする。真空ではない物質があるとどうなるか。金属のような導体では自由電子が大量にあるので分極はおこらなかった。
しかし、不導体（絶縁体）では原子が強く束縛されながらも回りにある電子の分布は変化できるので分極がおきる。これを誘電分極といった。
誘電分極があると分極した分子は電場の変化に反応して振動する。よって電磁波と相互作用し、エネルギーを交換できるわけだ。
これにより、光や電磁波は真空中より遅く伝達する。これを分散という。振動数の大きな電磁波ほど分散がよくおきる
さて、分極、分散の話は後に回し、今回は＋から出た電気力線がどのような振る舞いをするかみてみよう。
Q9.次のように原点を中心に、距離dだけ離れた電荷q1,q2がある時、原点から距離r、なす角θの位置にあるP点での電場のx、y成分を求めよ。
ただし、図のθ1,θ2を用いてよい。
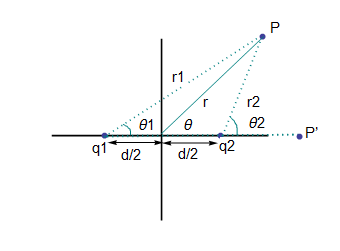
【図3-2】
上図の任意の観測点P(x,y)とすると電荷q1,q2がつくる点での電位はスカラーであったから式12から
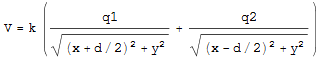
これを次のように微分すればどんな時も電場のx､y成分を求めることができた。まず式6に従って自分でやってみよう。
結果は次のようになる。今後よく出てくる形式なのでルートの中を微分するパターンをつかんでおこう。
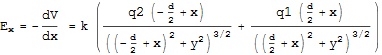
ここで図をよくみるとCosθ1,Cosθ2,次のように置き換えることができる。
では電気力線を表す方程式はどうしたらいいだろうか。
これまでの図では電気力線を矢印で表してきたが、実際には連続した線である。
電気力線をきれいに描くためにこれをMathematicaでシミュレーションするのは少々面倒である。
そこでウルフラムのサイトから次のプログラムを借りてきて実行してみよう。このプログラムの中身のは今は考えずに実行させてみてほしい。
【Mathematicaデモ】 Electric Field Lines Due to a Collection of Point Charges Contributed by: Timothy J. Atherton
(一部修正)
【実行可能7】
このプログラムでは電荷1,2の位置をマウスでドラッグして変えることができる。
さて、電荷を+1,-1に変えてみると+から出た電気力線が-に入ることがわかる。この時、+から出た電気力線の何割が-に入るかわかるだろうか。
答えはそのほとんどが-に入る。図は領域が限られるので無限に広げた図を想像するといい。
ただし、ほとんどと言ったのはx軸の負方向にのびる電気力線の振る舞いははっきりしない。無限大にいくものや、無限大からくるものは「特別」
なのである。このへんの事情は発展で考えることにしよう。
次に電荷1をq1=2電荷2を,q2=-1にして、まずグラフをよく観察してほしい。
さて、先と同じようにこの場合だと+から出たどれだけが-に入ることになるか、わかるだろうか。電荷が2対1だから電荷1の半分が電荷2に入る。
電荷1の極近くの表面では電気力線は等方的に出ているはずだから90°で空間をわければいい。
よく観察すると+から出ていく水平となす角が90°を超えるとその電気力線は-にたどりつけない。+から出る右半分の電気力線が-に入れるわけである。
さらによく観察するとq1からP点を通りq2に至る電気力線は下図のようにハートを横にしたような形を半分に切った線
になる場合がある。（Pの位置に依存する）
点Pから直線L上に垂線をおろし、この足をP’とするとPP’を半径にして円を描く。
この円を貫く電気力線の数を考えてみよう。
すると、このPの位置を同じ電気力線のどの位置にずらしてもこの数は変わらない！
電気力線は決して交わらないので下図の赤い円板内を通る電気力線の数は全部同じはずだ。
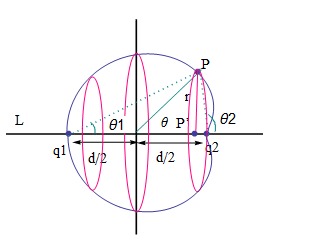
【図3-3】
そこでやや発展だが、この値が一定になるという内容を式にしてみよう。
これはq1をP点からみた時の角度 
からみた立体角と呼ばれるものを知っておくと便利である。
まずMathematicaの表現力を借りてこの立体角のイメージをマスターしてしまおう。これは普通の角度の立体版だ。
下図のように立体角は半径1の球を考え、この表面積で立体的な角度を表す。記号はΩ、単位は[sr]ステラジアンという。
下図で試してみると球の大きさを変えても立体角は変化しないのがわかるだろう。
では、ここで問題、全立体角はいくつになるか？
答えは簡単で半径1の球の表面積は 4πだからΩ＝4π[sr]である。
【Mathematica入力】 RevolutionPlot3Dは回転体を作図する。
【実行可能8】
ではq1からから出る電気力線はPから見る立体角を求めればこれに比例することになる。
では下図のように平面角θ1の時の立体角はいくつになるか？考えて見て欲しい。
図の球をPP’を半径とした円で切断したときのお椀型の表面積を出せばいい。できるかな？
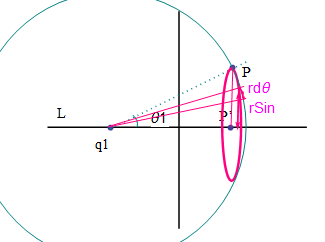
【図3-4】
上の図をよく見ると短い r dθ の幅で半径が rSinθ の円輪が下図のようにつくれることがわかる。
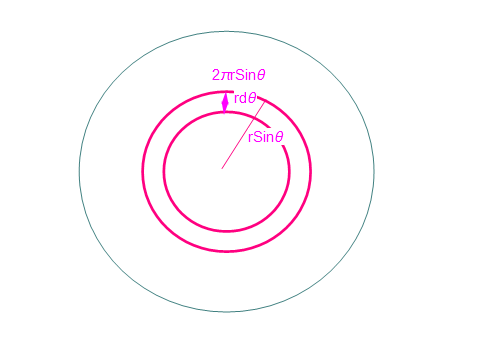
【図3-5】
そこで十分 rdθ が小さければ上の円輪も下の円輪も同じ長さとみなしてドーナツ部分の円輪の面積は円周の長さが 2πrSinθ だから
rdθ × 2πrSinθ
となることがわかるだろうか、この時のθは上の図の回転角ではない、横から見た時の角度であることに注意しよう。
すると求めるお椀の部分の表面積はこの円輪の面積を dθ をできるだけ細かく刻んで
θ を0から 
まで足し合わせればよいことになる。
この数学的な操作を積分という。r=1としてこの積分を実行すると
となる。これがP点から見た立体角なので電荷をqとすると電気力線の数Nは電荷を表していたから比例定数kとして
N = kq Ω
物理が得意な人は気づいただろう。全空間で考えれば電位力線の本数は全立体角の4πをかけて、
N = 4πkq
であった。今は部分的にこの本数を拾おうというわけだ。
複数の電荷が直線上にn個 並んでいる時は単純にの和をとればいいのでqとNが一定なら結局、定数をひとまとめにして
が得られる。よって図3-2の場合は次のような関係になる。
これが電気力線の式といえるものだ。この式もいくつかの大学入試で出題のネタになっている。
しかしここでは、 
ではなくてθだけで表したいから図の幾何関係を考えよう。
図3-2の場合はのように原点から両側に等距離離れてq1,q2の電荷があるから
これから
よって10式は次のようにかける。
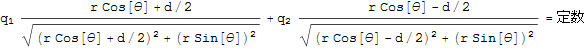
が得られる。少々複雑に見えるがこれは x=rCosθ, y=rSinθの関係からすぐにx､y座標に直せる。
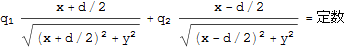
【Mathematica入力】
ContourPlot[ ]をつかってこのグラフを描かせよう。定数の部分を変化させて複数描くことができる。
前回のような複雑なプログラムはいらないのでMathematiaを利用したい人は中身もできたら理解しておこう。
【実行可能9】
電気力線の様子が詳細に表示された。はじめの表示を見ると＋から出た電気力線は-に入るものもあるが無限の彼方にいくものもある。
例えばq1=2,q2=-1とするとq1から出た丁度半分がq2に入る訳だ。よってq1から出た電気力線の内、鉛直よりq2側は全てq2に入り、反対側
の空間に出たものは無限の彼方へいくことになる。また、q1,q2の直線上の振る舞いは特殊になることもわかる。
この節の最後に3つの電荷がつくる電気力線の様子をMathematicaで紹介しよう。
【Mathematica入力】 Locatorをつかうと電荷の位置をマウスで直接ドラッグできる。
【実行可能10】
４．発展
電場と電位の関係が多少なりとも理解でき、その微分関係がグラフと共にイメージできるようになっただろうか。
ここではせっかくなので少々発展した話題を考えよう。
電位は力学的な位置エネルギーに対応し、U=qVが成り立った。つまり、山や谷が電位で、
その傾き(正確には傾きに-をつけたもの)が力学では力であり、電位に対しては電場であった。
実際に点電荷の場合はクーロンの法則は電位については
のように位置の大きさで割っている。この絶対値はあまりきれいではなく、処理も場合分けがいるので面倒になる。
例えば次のような原点に電荷がある場合のポテンシャルは絶対値(MathematicaではNorm関数)を使わないと、
場合分けをする必要がある。実際の物理は原点に電荷があり、電気的な山がそこにあるわけだ。
数学的にはこの電荷の境界で無限大が登場したり、発散したりする。
さて、電位を微分し、符号を変えれば電場が得られることを見てきた。しかし、高校ではベクトルとスカラーの区別が厳密ではなかった。
ここでは次のような演算子というものを定義する。
これを関数の左に作用させると微分をするわけだが、ベクトルをつくるのでx,y,z方向の単位ベクトル i,j,k をつけておく。
∇はナブラと読み、勾配をとる演算子である。MathematicaではGradというコマンドに相当する。
例えばこれをスカラーの代表例、長さｒに作用させてみよう。
Q10. 
求めよ。まず手計算すること。（ｘで微分する時はｙ、ｚは定数としてよい。）
【Mathematica入力】 次のように長さｒの勾配をとると結果はベクトル(３成分i,j,k)になる
つまり、
として ∇ｒ＝
でありこれはｒ方向の単位ベクトルである。
さらに
は
となる。これから絶対値等を意識することなく 
＝
を表していることがわかる。
これにkqをかければそのまま電場と電位の関係式で
E=-∇V
で表せばよいことがわかる。この表記はスカラーの勾配をとるとベクトルになるという内容も含んでいる。
で表す。ただし、∇がベクトルであったから∇どうしの内積で定義しよう。
新たにこの演算子を△で表し、ラプラシアンと呼ぶ。三角や逆三角が出てきて洒落ているが、きちんと国際的に通用する記号である。
内積で定義したのでこの△はスカラーであることに注意する。MathematicaではLaplacianというコマンドに対応する。
Q11. △ｒを求めよ。まず手計算すること。（ｘで微分する時はｙ、ｚは定数としてよい。）
2階微分するのだから0だろうと思うとそうはいかない。物理で △f=0 を満たすfは調和関数とよばれ、特別な意味がある。
【Mathematica入力】 Mathematica は次のように簡単に答えを出してしまう。
Q12.では宿題を出そう。△f=0 を満たす関数ｆ を3次元、2次元の場合について求めてみよ。
次の話題に変える。
電場、電位共に 
を分母に持つ。これは無限遠方で大きさが0になるためには便利な関数だ。
電場はn=2、電位はn=1 である。ここでは一般に
としてその性質をみておこう。。
【実行可能11】
デフォルトで実行するとn=2となっているので電場を表すが、実際のグラフは電位のような山の形になる。
逆にn=1とするとこの形は電場のものに近い。x軸の負のグラフが反転してくれれば正しい電位のポテンシャルを表す。
nが奇数の場合に山や谷にならず、偶数の時に山や谷になるのはどうも、数学と物理がずれているように見える。
さらにこの状態で指数を変化させてみてほしい。
指数が整数でない場合、定義域が全実数をとることができなくなっていることがわかるだろうか。
指数が整数になった瞬間に定義域は全実数をとる。（例外点があるが・・）
この突如の変化はどこから来るだろう。
これは例えばn=-0.5 でx=-2の時 
が実数で定義できないことによる。
そこでrを複素数に拡大してみたらどうだろうかいう疑問が湧く。数学でもおそらく複素数を学習したし・・。
虚部、実部の影響を変えられるように荷の強さを実荷q1,虚荷q2で区別しておく。
【実行可能12】
実行すると実荷を１とし、虚荷をとりあえず０として、指数4の場合が描かれる。4葉の立体が立ち上がる様子が見えてる。
この状態から指数を1とすると前回の電位のグラフが現れる。角度を変えて見てほしい、急な崖のある双曲線の立体版だ。
これを実軸で切り、射影すれば先とまったく同じ、正しくない(正の領域のみ正しい)グラフになる。
従って正しい、電位を再現していない。
ところがこの状態から虚荷を1まで上げてみてほしい。今までなかった虚数部分が見えてくる。
さらにここでマウスでグラフを下の図の視点になるようににちょいと回転させてほしい。ｘ軸の負の領域を特別と考え、
この部分は虚のグラフをとることにしたらみごとに電位を再現する！複素数の空間にできた図形をいろいろな角度で眺めてみると
実に興味ある見え方がある。現実の空間はこうした複素数の中の図形をある角度で切り貼りしたように実現されている。
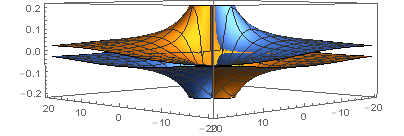
ｘ軸の負の部分は実は特別に意味をもつ。興味ある人は「Diracのひも」を検索してみるといい。
残念ながらその内容を理解するには高校以上の知識を必要とする。
再び、虚可を0にして見やすくしておく。次に指数負から正まで連続的にを変化してみるとおもしろいことが起きる。
グラフをよくみるとx軸の負領域は特異で指数を正の領域で上げるとこの特異な軸で葉は分裂して
その数が指数に近づくように変化する。指数の整数性はこの葉の数であることがわかる。
これは指数が負になっても変わらず、この特異なx軸の負領域には切れ込みがあり、
指数を連続的に変化させると指数の正負で凹凸が入れ替わるがこの切れ込みから葉が分裂、
合体して変化いくことが理解できる。実数だけでみていたときには指数の変化は不連続であったが、複素数でみると
連続した変化が見えるだろう。
虚荷の値を変化させた時には実のグラフはまったく無関係でないことも明らかであろう。
特に指数が負の領域で射影面を見ると波模様が見える。さらに指数を変化すると波の波長が変化していく。
虚数部分の影響がなめらかな波をつくるわけだ。これは現実にはエネルギーの散逸がおきている。
実は電磁気の現象を正しく理解するには複素数が自然に必要になる。
最後に大学で学習する複素関数の等角写像を利用し、先のグラフの実数部分をxに、虚数部分をyにしてxy平面を表すグラフを
Mathematica に描かせてみよう。
電気力線？のような図が見えてくる。指数を実部、虚部で分けて変化できるようにしたのでいろいろ試してみるといい。
ここで出来上がる図形が何を表現しているか？
君の想像力はおそらく、もっと学びたいと叫び出してきただろう。
【実行可能13】
ここでは一般的に指数をnとしたが電位や電場、あるいは万有引力もn=1,2を自然が選んだことにも実は深い意味がある。
今回の話にはまだ、磁場が登場していない。
参考文献
高校生では若干厳しいかもしれないが、基礎的な数学を理解していれば次の文献を電磁気学の入門として読破することを勧める。
John David Jackson Classical ElectroDynamics
「3.電磁気学」 中村 哲・須藤彰三 朝倉書店
ファインマン物理学〈3〉電磁気学 岩波書店