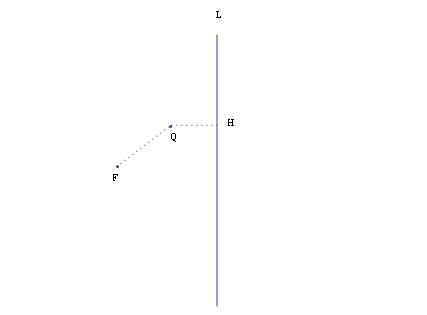
Mathematicaを利用した物理 双曲線
H.Yanase
このシリーズはMathematicaを利用すると自分で変更し、試行錯誤できるようになっているがMathematicaがなくても理解できるように作成されているMathematicaのプログラムに興味がない読者はプログラム部分はとばして結果だけを見ればよい。Mathematicaの入力は【Mathematicaの入力】で区別する。Mathematicaがインストールされていれば全てのコマンドは修正、実行が可能であるが理解に必要な結果はCDF(WolframのHPから無償ダウンロード可能)をインストールすればWebページからも実行できる。これを【実行可能】で表す。(PCの環境によってはプログラムロード、実行に多少時間がかかる場合があります。)
Mathematicaを利用する場合は事前にMathematicaの基礎(本HPからダウンロード可能)を読んでおくとよい。
本章ではMathematicaVer8から機能強化されたマウスなどによるダイレクトな入力方法の学習もできるようにしてある。
より細かなプログラムの説明はMathematicaのHPにチュートリアルとして豊富なコンテンツがあるので参考にするとよい。
Mathematica HP:http://www.wolfram.com/
筆者HP：http://www.ne.jp/asahi/buturiwa/ai/EducationM1.htm
楕円(Ellipse)、放物線(Parabola)、双曲線(Hyperbola)は物理の運動の分野や波の分野でとても重要な曲線である。
数学的にはこれらは1つの仲間で次のようなパラメタで統一的に表現できることを示そう。
図のように直線Lとある決まった点Fがあるとする。Qから直線Lへの垂線の足をHとしよう。
ここでQF/QHの比をeとして例えばe=1となるようにQ点を動かすとどんな線になるだろうか。
H=(0,y) Q=(x,y) F=(a,b) とおこう。
すると線分 
QH=x とすると
となるので
から 
よって 
+b
作図すると次のようになる。
【Mathematica入力】
下記の例でClearというコマンドは記号を初期化させるためのものでなくてもよいが、Mathematicaでこのコマンドを実行する以前にこの記号に値を代入したりしているとそれを記憶しているので初期化している。はじめて使う場合は必要無いが長く計算させていると以前の結果が代入されていることがあるので間違いを減らすためのおまじないみたいなものである。；があるとそのコマンド結果は表示されない、すっきりさせたい時に利用する。実行はShift+Enterキーだ。
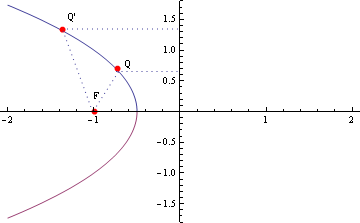
これは普段に見るものと90度回転しているが放物線である。e=1なのでルートの中を展開すると
=
となるので 
xとyを変えれば見慣れた放物線になる。
そこでこのeのことを離心率と呼ぶ。
ではe<1の時はどうなるだろうか。この時ルートの中は 
が正として残り e>1の時はルートの中の 
が負として残ることがわかるだろう。この違いはe<1の時に、楕円。e>1の時に双曲線という結果になる。そこでeを変化させてグラフを描かせてみる。
【Mathematica入力】
次のようにMathematicaではManipulateのコマンドで変数を動的に変えることができる。
最後のAppearance→”Labeled”は離心率の値を画面に表示させるオプションである。
【実行可能CDF1】
楕円、放物線、双曲線がeをパラメタとして連続的に変化することが確認できただろうか。
これからe=1で放物線、0<e<1で楕円、e>1で双曲線になることがわかる。
これは物理においても例えば人工衛星は地球の周りを楕円軌道している。この衛星に搭載しているエンジンを噴射させ、地球の軌道を離れ、他の惑星に行かせたい時にはその軌道をいったん双曲線になるようにしないといけない。楕円である限り閉じた曲線になるわけだから必ず戻ってきてしまうわけである。さらに地球上で石を投げるとこれは高校で学習したように放物線を描く。その結果地球に落ちてくる。では地球に落ちるよりはやく地球を回るようにすごい速さで投げ出したらどうなるか。答えは人工衛星のになり楕円軌道を描くのである。楕円軌道を描くのに必要な速度、そして双曲線、つまり引力圏を離脱するのに必要な速度も高校の物理学で簡単に求まるのである。
次にこの関係を立体的に見てみよう。非常におもいろい図形「円錐」をもってきてこれを平面で切り、その切り口を観測するとここにも楕円(円)、放物線、双曲線が登場する。
【Mathematica入力】
はじめに次のように切り取る板をθの関数で定義する。
例では外枠、座標軸、等高線を全て消すように指示している。
次のことを考えて、面の角度をしていし、描画領域を決めておく。
(参照)
http://demonstrations.wolfram.com/にはWeb上でも実行できるプログラムが多く掲載されている。また数学のデータベースも充実している。Mathematicaがあればこれらは「ヘルプ」メニューから検索ができる。からないコマンドが出てきたらその単語の上にカーソルを移動し、f1キーを押すとMathematicaの説明が見られる。
"Conic Sections: The Double Cone" from the Wolfram Demonstrations Project
http://demonstrations.wolfram.com/ConicSectionsTheDoubleCone/
【Mathematica入力】
次のように入力するとマウスで自由に回転する板が得られる。[ ]の中には0からπまでの値を入れると面が傾く。
【Mathematica入力】
次のように入力するとマウスで自由に回転する3次元の円錐が得られる。
【Mathematica入力】
先の円錐のプログラムを切り取る板の角度に依存させ、次のように定義する。MeshFunctionを利用し、切り口の部分を太線で強調させる。
次にManipulateでこの円錐と板を両方描かせ、角度をマウスで指定できるようにする。ここまでのプログラムを以下には1つにまとめてある。
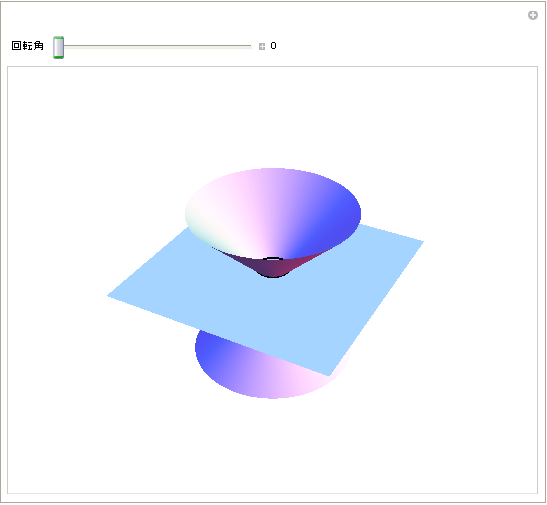
マウスで全体を動かし、スライダーで切り取る口の角度を変更してみよう。特に放物線を見つけるのは難しい。
どんなときに円、楕円、双曲線、放物線になるかが確認できただろうか。円錐の頂点から直線をまっすぐおろした線を母線という。この母線に平行な平面で切った切り口が放物線になる。このことを確かめてみるために先のプログラムを変更してみよう。
【Mathematica入力】
各関数に平面の高さhを変数に加えて定義しなおす。そして答えを表示させるチェックボックスをつけてチェックがある時にはIf[ ]関数で分岐する処理を加えた。これらの処理もMathematicaでは極力簡単にできるように工夫されている。
関数の定義は適当な名前[a_,b_]:=f(a,b)という形で引数をいくつにしても任意の関数を定義できるがManipulateを使う場合はInitialization:→以下に定義しておく。Appearance→”Labeled”オプションをつかうと例のように選んでいる数値が横に表示される。
オプションのControlType→は選択ボタンをチェックボックスやラジオボックス等選べる。この場合は排他的に選択するのでSetterBarとした。複数選択可にする場合はTogglerBarを使うとよい。これらの機能の紹介もヘルプやチュートリアルに詳しい。
【実行可能CDF2】
選択なしを選んでおくと角度も自由に変えられる。例えば放物線を選ぶと円錐の母線と面が平行になるので高さを変化させれば放物線が変化するのがよくわかるだろう。マウスで全体をドラッグして平面が線になる角度でためしてみるとよい。この変化の中に宇宙の運動の全てが記述されるわけだ、小宇宙をじっくり観察してほしい。
では次に平面に点A(-p,0)、B(p,0)を決めて適当な距離Q(x,y)を動かす。この時、距離AQ、BQの和が一定になるようなQの軌跡はどんな曲線になるだろうか。考えてみてほしい。
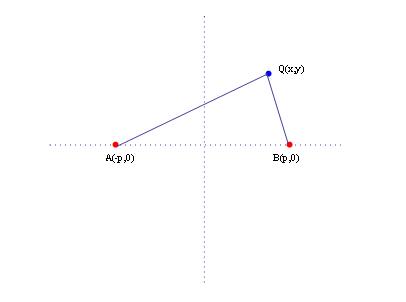
これは実験すれば解が得られる。たるんだ糸のはしをA,Bとして固定し、細いペンで糸をピンと張るようにして線を引いていけばいい。結果はやってみると次の図のような楕円ができる。
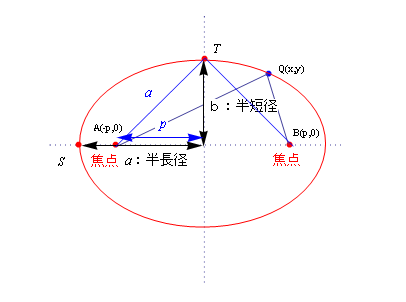
そこで図のように半長径をa、半短径をbとする。そして糸を固定した点A、点Bを焦点と呼ぶことにする。
惑星の運動は太陽を1つの焦点としてこの楕円軌道を描いている。また、作図した楕円の線に沿って壁を作成し、1つの焦点からビー玉をはじくと必ずもう一つの焦点を通る。さらにこの壁を内側を鏡にして１つの焦点に電球をおけば、もう一つの焦点に光が集まり明るくなることからこの「焦点」という名前が使われている。
【宿題1】
焦点からスタートし、楕円面にビー玉が衝突する時の入射角はどこでも等しくなることを示せ。
この作図で本当に楕円ができるなら高校でならった楕円の方程式が導けるはずである。それを示そう。
ペンをS点に持ってくると糸の長さは2p+2(a-p)=2aとおける。
図の線分ATの長さが丁度糸の半分のaになることがわかる。よって三平方の定理から次が成り立つ
次に
,
だからAQ＋BQ＝2aだから
+
=2aとなる
=2a-
の両辺を2乗し、
+
よって 
=
となるのでもう一度両辺を2乗すると
となるから簡単にすると
を得る。これに式(2)を代入すると
a>0,b>0として両辺を 
で割ると
となり見慣れた楕円の方程式(a=bならば円の方程式)が得られる。
円はa=bと考えることができるからこの時、式(2)からp=0、すなわち円は2つの焦点が重なり１つになった状態と考えられる。
【問題1】
さきほどの離心率eを長半径aと短半径bで表してみよ。
【解答1】
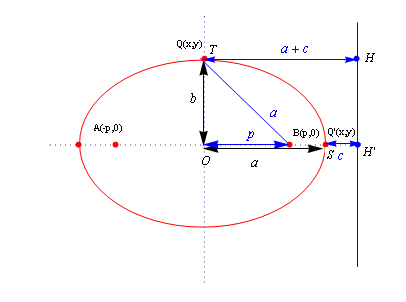
下図のようにQがTの位置にきた時をT=Qとし、図のSの位置にきた時をS=Q’とする。
また、SH’=cとするとTH=a+cである。はじめにT=Qの時
である。よって式(1)より次のように離心率が求まる。
次にQがSにある時は次のように離心率が求まる。
離心率はどこでも等しいから式(5),(6)より
この結果を再び式(6)に入れると式(2)より次のように解が得られる。
またこれから離心率は焦点の位置pが
p = a e...(9)
で与えられることがわかる。
【問題2】
問題1の結果を利用してe=1となるのはどんな特徴の曲線か考えてみよ。
【解答2】
問題1の結果からe=1とするとp=aとなる。すなわち図の焦点は曲線上に移動してしまうのでもはや楕円ではない。式(8)からこの時、b=0になってしまうので横幅が無限に長いような細長い楕円になってしまう。しかしe=1となるのは楕円であることをあきらめれば曲線の外に焦点を持つ場合で答えがみつかる。
これは下図のようにはじめに触れた放物線である。原点をOとして高さhのところに焦点Pがあったとしよう。
曲線上の点をQ(x,y)とおく。直線までの距離QHとPQが等しくなるような曲線を求めればよい。
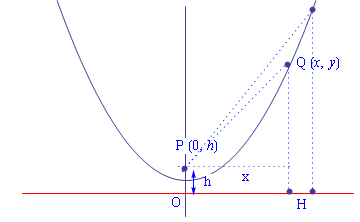
そこでQ(x,y)とするとPQ＝QHが成り立つので図のように点Pと直線との距離をｈとすると
より
となるので答えは放物線であり、しかも焦点の位置は頂点と原点までの2倍の高さの位置にとればいいことがわかる。
このようにp=aとならないところに奥深さがある。
放物線はPQとQHが等しくなるようにQを動かした時にできる曲線であるといえる。放物線や双曲線と異なり焦点は1つである。
ある意味で2つあった楕円の焦点が無限大まで離れて1つしか見えてない状態といえる。
【Mathematica入力】
ここでMathematicaを利用して焦点の位置を自由に動かした時、ダイレクトに楕円の変化がわかるプログラムを作成してみよう。
楕円の作図には様々な方法がある。極座標というのを用いるのが簡単だがここでは焦点の位置をはっきりさせるため式(4)を用いよう。 式(2)(4 )から
焦点の座標は離心率を用いて式(9)で決まるから式()からbを消して
となることを利用する。
【実行可能CDF3】
焦点を表す小さな灰色の円（ロケーター）が現れたはずだ。これをマウスで直接ドラッグしてみよう。
楕円と焦点の関係を色々動かしてためしてみるとよい。
では次に平面に点A(-p,0)、B(p,0)を決めて適当な距離Q(x,y)を動かす。この時、距離AQ、BQの差が一定になるようなQの軌跡はどんな曲線になるだろうか。考えてみてほしい。
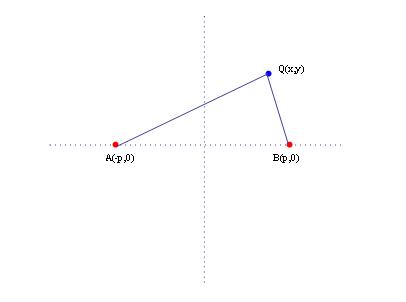
そこでQ(x,y)とするとAQ-BQが一定になるわけだから
より次のようにおける。
2乗すると
再び2乗すると
ここで簡単にするために 
を選ぼう。すると
となる。これは 
の時は
となる。これは一般に双曲線の方程式である。
の時は次の楕円の式になる。
kをもどしてyについて解くと次を得る。
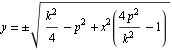
【Mathematica入力】
これをpを変数にしてMathematicaに描かせてみよう。簡単に視覚に訴えるプログラムがMathematicaの特徴だ。
だたこの場合は単純にyの値を描画させてしまうとルート内の符号によって楕円も描いてしまうのでPlotのオプションにある
RegionFunctionをつかう。このオプションは描画領域を指定することができる。まず次のコマンドでこの式のｘ軸との交点を
みつける。もちろんｙ=0としてｘについて解けばいいので手でやっても簡単な結果が得られる。
Mathermaticaでは方程式を解くには次のようにSolveコマンドを使う、下記の例ではさらにSimplifyに条件を入れて簡単にした結果を得られるようにしている。
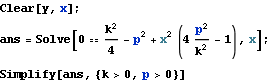
Mathermaticaでは方程式を解くには次のようにSolveコマンドを使う、下記の例ではさらにSimplifyに条件を入れて簡単にした結果を得られるようにしている。条件は式以外にも実数や複素数を指定することができる。
ではプログラムを書くと ±の2つの解を{}で同時に描かせる。ただし、焦点の位置pと距離の差ｋは選べるようにする。
ｐについては画面から直接入力できるようにLocatorを使って指定する。ただし、2つの焦点は別々に動かすことができるのでそれぞれの焦点について2種類の双曲線が描かれるようになっている。1つにしたい時はpをp[[1]]に置き換えると1成分だけをとるので1組の双曲線しか現れない。RegionFunctionを用いて先の結果からｘが-k/2とk/2の範囲は楕円になるので描画しないようにしている。
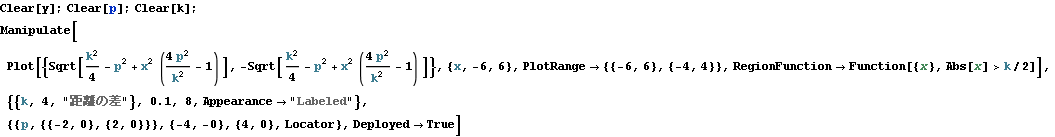
【実行可能CDF4】
さて、物理を学習しているならこのグラフを見てあることに気づくはずだ。水面波が2点ＡＢから同位相で出ているとき、十分時間がたつと合成波ができる。このとき距離の差が行路差に相当しこれが波長の整数倍なら強めあうという干渉条件があった。つまり、この双曲線は節、腹線そのものだ。
距離の差kがn=1,2,3.....として
k = AQ - BQ = nλ...(11)
を満たすのが強め合う腹線なのでこれをMathematicaに描かせる。kをnλに置き換える。焦点は1つを選ぶようにしてンnとλの組み合わせによっては楕円が描かれることを許している。
では最終的にA,Bからの波の波面を同時に描かせてみよう。これには以下のようにプログラムを変える。
【Mathematica入力】
g1に先の双曲線を入れて、g2にはA,Bから半径がλの整数倍になる円形波を描かせる。そしてチェックボックスckがチェックされるとこの円と双曲線が両方表示されるようにする。円が正しくみられるようにオプションとしてx､yが１対１になるようにしている。
【実行可能CDF5】
このプログラムでは選び方では楕円も描画される。しかし、波源を動かせば双曲線がすぐに現れると思うので大きなn
と小さなλを選んで双曲線が多く描けたら波面表示のチェックボックスをマウスクリックするとみごと両方の波の円の交点、つまり山と山が重なっている点を双曲線の群が通過していることがわかる。いろいろ確かめてほしい。
さて、実際にお風呂場で水面を2カ所でとんとんとたたいてみると円形波ができて、しばらくすると合成波になる。
１箇所をとんとんとたたいた時はきれいな円形波が波紋として広がっていくのがわかる。しかし、2カ所でたたい合成波をみた場合、
ここであつかったような節線、腹線を見ることができるだろうか。2カ所にすると波紋のふち、つまり円形波の円周部分も波打ち、節線、腹線を見るのは難しい。しかし腹線は常に振動しているため見るのは難しいが節線であれば確認できそうなものである。
この様子をMathematicaでシミュレートしてみよう。
【Mathematica入力】
Norm[A,B]関数はA,B間の距離を出す関数である。また、波の干渉ではなめらかさを出すためにPlotPointsのオプションに
まるめ関数Round[]をつかって波長に応じた解像度を出すようにしている。
【実行可能CDF6】
実行画面になったらまず、位相のプレイボタンを押して水面波が動く様子を確認してみよう。マウスでドラッグすると動画を回転させることができるが負荷が大きいので一度停止ボタンを押してから回転させてみるとよい。
このプログラムでは波源AB間を６になるように最初の設定がなっている。波源１の座標のスライダーを変化させるとこれを変えられる。また、A,Bの波源の位相がπずれるように波源１の振幅と波源２の振幅はマイナスの関係にしてある。位相がπずれていれば中点は必ず節になるはずだ。
さて、動きが確認できて、どこに節線があるか予想してみよう。節腹線表示チェックを入れると赤線で節線が出てくる。
節腹線は合成波の速度の向きを表していた。
確かに節線は常に高さ０になっていることが角度をかえてみると確認できる。
振幅を同じにすると節線と腹線が入れ替わることもわかるだろう。また、どちらかの波の振幅を0にするときれいな円形波が確認できる。でももう一つの振幅を0から増やしていくと円形の淵も波打ち合成波に移行していくのがわかる。
注意：このプログラムでは楕円を消す処理をしていないのでλ、ｎの選び方によっては楕円が出てくる。
さて、波の干渉を注意深く観察すると波源ABを結ぶ直線上は特別であることがわかる。波源A,Bの内側ではお互いの波は反対向きに進むので合成はは定常波となり進行しない。しかし、波源の外側ではAの波もBの波も同じ向きに進むので合成波も同じ向きに進む。
この様子もシミュレートしてみよう。
【Mathematica入力】
先の立体図を波源ABで切った断面を表してみよう。
以下の例ではGrid[]コマンドを用いてグラフを3段で表示させている。
1段目にはAからの波とBからの波の進行波が描かれ、振動数を入力できるようにしてある。rcがかかっているのは進行方向を反転させるためである。
2段目にはAの波とBの波の足し算した波が描かれる。
3段目には波のエネルギーや強さが振幅の2乗に比例したからAとBの振幅の和の2乗を表すようにしてある。外側←→内側のスライダーでrcを１と\:ff0d１に交換させ波の向きを同じ向きか反対向きになるようにしてある。ManipulateにAppearance→”Open”のオプションを加えると例のように再生のボタン等が+をクリックしなくても表示された状態になる。
【実行可能CDF7】
実行画面になったらプレイボタンを押してみよう。
Aからの波とBからの波が同じ振動数で向かい合い、下にはその合成波が描かれている。
外側←→内側のスライダーを反対にすると同じ向きになり、外側の合成波が下に描かれる。
さらに振動数を変化させてみよう。複雑な形になる。様子が確認できたら１の振動数を１０，２の振動数を９くらいにしてみよう。高校で学習したうなりの様子がみえる。非常に激しい振動数＝(10+9)/2=8.5Hzとゆっくりの振動数(10-9)/2=0.5Hzとなる。
人間は低い方のうなりつまり0.5Hzの方が聞こえやすい。そしていったんこの音を聞くと他の音はきこえなくなる。さらに振動数が低いと人は音の強さで聞くので3段目のグラフで見るように振動数が2倍つまり0.5×2=1Hzの音がうなりとして聞こえるわけだ。
MathematicaにもPlayという音を出すコマンドがある。これで10ヘルツのうなりと10ヘルツのSin波の音を聞き比べてみるといい。
内側外側のスライダーを入れ替えると合成波の速さも極端に変化するはずだ。注意すべきは合成波の速度は波長（振動数）が異なると速くにもみえたり、遅くにもみえたりする。しかし、どちらかの波をけせば常に波は一定の速さ進行しているだけだ。同じ向きに速さが重なっても同じ速さの波ができる。
では波源A,Bからの任意の位置Qで合成波の速度はどうなるだろうか。波の速さはV=f λ で決まった。波源からあらゆる向きに等しくこの速度の波が出ているわけである。注意すべきは波の速度は振幅に無関係で基本的にＡ，Ｂから出た波の速さは等しく、次の図のように平行四辺形の法則で簡単に合成される。
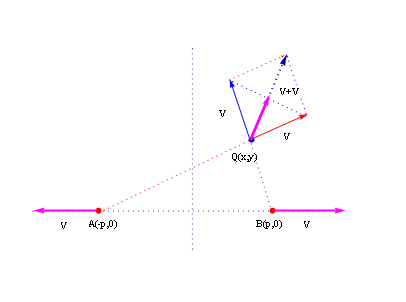
しかし、ここで注意がいる。合成された速度の最大は元の波の速度を超えることはない。従って合成V’は簡単には
となることだ。これは運動量保存則を用いると媒質の質量をｍ、速さをＶとして同じ向きなら
反対向きなら
で動かないことがわかる。（実際の波の場合はこんなに簡単ではない）
ではこの様子を Mathematica に描かせよう。
【Mathematica入力】
はじめに2つの焦点が現れるが左の焦点をマウスでドラッグすると波源の位置A,Bがともに対照的変化する。右の焦点は任意の位置に動かすことができる。そして速度ボタンを押すと赤いベクトルで合成速度が表示される。
また高校でならったようにこの合成速度は節腹線に一致するので節腹線ボタンを押すと節腹線が現れる。
波長や数ｎを変えることができるが楕円を消す処理をしていないのでそのまま楕円が現れることに注意すること。
【実行可能CDF8】
さて、いろいろ試してみるとおもしろいことに気づく。前にもふれたように波源AとBの直線上は興味ある現象が起きている。
A,Bを越えた瞬間に速さが0から最大になるのだ。他の位置で速さが最大になるのはどこだろう？
そう、答えは無限大遠方でしかない。つまり直線AB上でA,Bの外側の半直線は無限遠と同じなのだ！さてこれはどういうことだろう。宿題としておく。
