LecPic.html

戻る　画像解析入門 with Mathematica
\:ff5e高校生の挑戦シリーズ４「波と粒子」\:ff5e

　メニュー
１．色とは
２．光とは
３．デジタル解析

本講座はMathematicaを利用して画像解析をしようとするものである。
対象は高校卒業程度であるがこだわらない、時として大学程度の数式も登場するが数学や物理に興味があるもの、手元にMathematicaがあるものは挑戦してほしい。また、Mathmatica がなくても高校で習う物理や数学の理解を深めることが可能なように配慮した。高校数学の「微積分」と「三角関数」の基本を卒業したら挑戦してして欲しい。

Mathematica について不慣れな人はまず前講座の「Mathematicaの基礎」を一読することを勧める。
微積分に自信がない人はまず前講座の「微積分の基礎」また「微分方程式と運動方程式」を一読することを勧める。
また、本講座は前回の「音声解析入門」を一読してから読むことを勧める。

Mathematicaがない場合でも以下のサイトからMathReaderを無料でダウンロードしてくればMathematicaと同じようにアニメーションや３次元の回転などが可能である。Mathematica は高価なソフトである。同じような数式処理が可能で無償のソフトもいくつかある。(巻末参照)しかしその表現力と研究にもたえ得る能力の高さからこのソフトを中心にここでは話が進む。何より高校生用には格安のバージョンが用意されているのでもし、君が高校生なら今のうちに利用したほうがいいだろう。詳しくは以下のサイトを参照してほしい。
【 Mathematica 】http://www.wolfram.com/
Mathematica はウルフラム・リサーチ社の製品である。2005年現在での最新バージョンは5.2である。
本文中Mathematica に入力する部分からは【 Mathematica 】と見出しをつけた。

Mathematicaのコマンドの最初は必ず大文字から始まり[]の中に内容を入れる。
また、範囲の指定には必ず{　}の中に入れる。入力は全て半角英数を用いること。
◇　Mathematicaの入力はShift+Enter
◇　改行したい時はEnterのみ

　はじめに

　デジカメや携帯電話で気軽にデジタル写真が撮れるようになった。miniSDカードやXDカードのような小さなメディアにたくさんの写真が記録できる。これらは写真をいかに人間の見た目で画質が落ちないように圧縮して画像ファイルのサイズを小さくするかの技術による。パソコンで画像を開き、ファイル名の詳細を見ると.BMPや.JPG、さらには.GIFや.TIFFなど同じ画像でも多くのファイルの種類がある。ファイルの圧縮のしかたにもいろいろな特徴があるのだ。ここでは簡単な画像処理を紹介しながら色や形についても学んでみよう。

１．色とは

　物理では色は光の波長によって決まることを学習した。だいたい人間の目に見える色はおよそ４００nmから８００nm程度である。（nmはナノメートルと読み１nmはウイルス程度の大きさになる。1mを１０の９乗で割ったのが1nm)
波長が長い側が赤色で波長が短い方が紫になる。青より波長が短いとこれは紫外線となり人の目には見えない。逆に赤より波長が長いと赤外線となりこれも人の目には見えない。ただ他の生物ではこの領域の色を感知するものがいる。紫外線はエネルギーが高くなるので化学変化に関与し、赤外線の方は物質の温度と関係していた。色には３原色がありこの色を混ぜると様々な色をつくることができた。まずPCをパレット代わりに用いて色をつけることをみていこう。

Mathematicaでの色操作の基本

【 Mathematica 　】　
Mathematicaでは次のようにRGBColorを用いて簡単に図形に色をつけることができる。　Rは赤、Gはグリーン、Bは青である。はじめにMathematicaの色操作を練習しておこう。

Show[Graphics[{RGBColor[0, 0, 1], Rectangle[{0, 0}, {1, 1}]}]]

[Graphics:HTMLFiles/LecPic_2.gif]

◇RGBColor[赤, 青, 緑]、色をRGB関数でつける。赤、青、緑のところには０から１までの数字を入れる。
◇Rectangle[{x1,y1},{x2,y2}]対角線の座標が(x1,y1),(x2,y2)の長方形を描く。

RGBColorの数値を変えて自分で他の色の四角形を描いてみるといい。

ここでは１つの色は２５６通りの強さを持たせることができる。次のようにして自分の目がその色の差を区別できるか確かめてみよう。そのまえに色の強さを変えて四角形を描かせるプログラムを入力しておこう。

【 Mathematica 】　
では連続的に色を出す関数を次のように定義してみよう。

$TBR[imax_, n_, d_] := Table[{RGBColor[(i + n)/255, 0, 0], Rectangle[{i/(d * imax + 1), 0}, {(i + d)/(d * imax + 1), 1}]}, {i, 0, imax, d}] ;$

$TBG[imax_, n_, d_] := Table[{RGBColor[0, (i + n)/255, 0], Rectangle[{i/(d * imax + 1), 0}, {(i + d)/(d * imax + 1), 1}]}, {i, 0, imax, d}] ;$

$TBB[imax_, n_, d_] := Table[{RGBColor[0, 0, (i + n)/255], Rectangle[{i/(d * imax + 1), 0}, {(i + d)/(d * imax + 1), 1}]}, {i, 0, imax, d}] ;$

☆TBR[最大差,始点,増分]
これは赤（TBGは緑、TBBは青の最大差（２５５より小さくする）をいくつにして、始点（２５５段階のどこから始めるか）を決め、増分（最大で最大差の値）だけ四角形の色の強さを変えて描いている。だから最大差＋始点が２５５を超えないようにしよう。例えば最大差を100で150からスタートし、差を１０ずつで刻むと次のようになる。

[Graphics:HTMLFiles/LecPic_9.gif]

[Graphics:HTMLFiles/LecPic_10.gif]

[Graphics:HTMLFiles/LecPic_11.gif]

１０段階で刻むとさすがに色の判別はつくね。ではこれを５段階にしたらどうかわかりやすくするために２つの長方形にしよう。

[Graphics:HTMLFiles/LecPic_15.gif]

[Graphics:HTMLFiles/LecPic_16.gif]

[Graphics:HTMLFiles/LecPic_17.gif]

前回の音のところでも１Hzの差はほとんど聞き分けができなかった。同じように個人差にももちろんPCの性能にもよるが色の変化も小さくなると区別はつかないね。
では自分で５のところを小さくしていってどこまで区別がつくか試してみよう。

連続的に最大の変化をつけるグラデーションは次のように作ればよい。

[Graphics:HTMLFiles/LecPic_19.gif]

256通りというのは実はのことである。この２の何乗かという数字をビット数という。よくパソコンの色の説明で8ビットカラーとか16ビットカラーとかいうのはこのことだ。ただしRGBで３色あるから全部で何通りの色が出るかMathematicaで計算すると次のようになる。

【 Mathematica 】
◇N[値、桁数]、Nは数値にしろという命令である。、桁数をつけると何桁まで出せという命令になる

約17万色も色が出るし、少なくともパソコンにはこれだけのメモリがないと８ビットカラーは扱えない。MathematicaはRGBだけでなく色を表現するのにHue関数があるこれは前回の音声解析のところでも扱ったように０から１までの数字で赤色から紫、そして赤まで一巡するようになる。先のRGBをこのHueに書きかえて色のチャートを作るために次の関数を入力してみよう。

$HUC[imax_, n_, d_] := Table[{Hue[(i + n)/255], Rectangle[{i/(d * imax + 1), 0}, {(i + d)/(d * imax + 1), 1}]}, {i, 0, imax, d}] ;$

全ての色を出ためには次のようにすればよい。

[Graphics:HTMLFiles/LecPic_25.gif]

色の３刺激値

光は３原色があればどんな色を作ることができたそれは次のようになる。これをパソコンではRGBで混ぜているわけだ。ただし絵の具を混ぜるとこれとは異なる。全部混ぜたら黒くなる。光の場合は白だこの関係を補色という。さて、色は人間の脳が認識している。実はその働きはそう単純ではない。人間がある色を刺激として与えた時にどれくらい強く感じるかをグラフにしたデータがある。これは詳しくは民族や地域によって異なるが平均的なものは色の３刺激値として理科年表にものっている。以下でこのデータをMathematicaに取り込む方法を示そう。自分たちでも実験したデータを一度テキストファイルにしておけば簡単に取り込むことができる。

[Graphics:HTMLFiles/LecPic_26.gif]

【 Mathematica 】
◇Import["ファイル名","形式名"] ファイル名（フルパス指定）を形式に変えて読み込む

理科年表ｘｙｚ表示の３刺激値のデータをデキスト(タブ区切り)でRGBのそれぞれdataR.txt,dataG.txt,dataB.txtという名前にしてD：ドライブのルートに保存する。（保存場所は他でもいいがその場合は下記のD:のところに自分のデータの保存先のパス名を入れること。実験データもこの方法でMathematicaに簡単に取り込むことができる。
以下ではInterpolation補完関数を用いてデータのないところもなめらかな曲線になるようにしてある。次のセルをShift+Enterで入力しよう。同じような名前があると警告が返るが無視してよい。

Plot[{fr[x], fg[x], fb[x]}, {x, 0.37, 0.7}, PlotStyle -> {{RGBColor[1, 0, 0]}, {RGBColor[0, 1, 0]}, {RGBColor[0, 0, 1]}}] ;

cR[x] = Abs[fr[x]]/Max[fr[x], fg[x], fb[x], 0.00001] ; cG[x] = Abs[fg[x]]/Max[fr[x], fg[x], fb[x], 0.00001] ;

[Graphics:HTMLFiles/LecPic_37.gif]

グラフの横軸は波長（μm マイクロメートル　1μm=m)である。
単純に波長が長いと赤と感じるのではなく、人間は上のグラフを見ると波長の小さい領域でも赤を感じている小さな山がある。しかしここではより青を強く感じるのでやや紫にみえるのだろう。緑の裾のはとても広く広がっている。こともわかる。
次に上のデータを元にして最初の色のチャートを出す関数を応用し、実際上のグラフを色にして表現してみよう。
どんな関数を作ったらよいか次の例を見る前にまず自分で挑戦してみるとよい。

TB = Table[{rgb[0.38 + i/10], Rectangle[{i + 0.1, 0}, {i + 4/255 + 0.1, 1}]}, {i, 0, 4, 4/255}] ;

[Graphics:HTMLFiles/LecPic_42.gif]

うまくいったかな？これで波長を変化させた場合の色チャートができた。
約0.38μmより波長が小さいと紫外線の領域で人間の目には見えないし、約0.78 μmより大きいと赤外線の領域で同じように人間の目には見えない。虹が7色というがかなり曖昧であることもよくわかる。
ここでは新しく波長で色を表す関数rgbも定義したので自分で波長を入れて試してみよう。
例えば黄色は次のように約0.58 μmを入れればいい。同じ黄色でも非常に多様であることがわかるだろう。

Show[Graphics[{rgb[0.58], Rectangle[{0, 0}, {100, 50}]}]] ;

[Graphics:HTMLFiles/LecPic_44.gif]

色の3原色は平等ではなく偏りがあったり混ざったりしていることがわかった。それ以外にも「彩度」や「明度」によっては強く感じるところがあり色の錯覚が生じる。次にこの様子を見てみよう。

色の錯覚

それでは背景と実物がもっとも目立つ色の関係はどうなっているだろう。次の2つの円は同じ色で描いたものだしかし、背景が異なることでかなり違った印象を受ける。

[Graphics:HTMLFiles/LecPic_45.gif]

次のセルをShift+Enterで入力したらｒ、ｇ、ｂの値を色々変えてみよう。
ちょうど背景がRGBの値が１から引いた値で塗られている。こういう関係を補色という。

r = 1 ;
g = 0 ;
b = 1/2 ;
gh = {RGBColor[r, g, b], Rectangle[{0, 0}, {1, 1}]} ;
g1 = {R ... or[1 - r, 1 - g, 1 - b], Disk[{1/2, 1/2}, 1/6]} ;
Show[Graphics[{gh, g1}], AspectRatio -> 1] ;

[Graphics:HTMLFiles/LecPic_47.gif]

上の図を30秒くらいじっとにらんで白いところを見るとなんと色が反転して見える。錯覚の１つだ。だからポスターの文字は補色をとるとかえって見ずらくなる。

さらに次のプログラムをShift+Enterで入力したら図形のセルをグループ化してCTRキーとYキーを同時に押してみよう。アニメーションができる。中央の黒●をじっとみているとありもしない色が見えてくるぞ。これも補色の効果だ。
........................................................................................
PCの性能によってはグループ化したセルで右クリック、オプションインスペクタを開いてグラフィックスのAnimatoinDisplayの値を0.5程度にしてみよう。

gh = {RGBColor[4/5, 4/5, 4/5], Rectangle[{0, 0}, {1, 1}], RGBColor[0, 0, 0], Disk[{1/2, 1/2}, 1/18]} ;

Show[Graphics[{gh, g1, g2, g3, g4, g5, g6, g7}], AspectRatio -> 1] ;

Show[Graphics[{gh, g2, g3, g4, g5, g6, g7, g8}], AspectRatio -> 1] ;

Show[Graphics[{gh, g3, g4, g5, g6, g7, g8, g1}], AspectRatio -> 1] ;

Show[Graphics[{gh, g4, g5, g6, g7, g8, g1, g2}], AspectRatio -> 1] ;

Show[Graphics[{gh, g5, g6, g7, g8, g1, g2, g3}], AspectRatio -> 1] ;

Show[Graphics[{gh, g6, g7, g8, g1, g2, g3, g4}], AspectRatio -> 1] ;

Show[Graphics[{gh, g7, g8, g1, g2, g3, g4, g5}], AspectRatio -> 1] ;

Show[Graphics[{gh, g8, g1, g2, g3, g4, g5, g6}], AspectRatio -> 1] ;

２．光とは

　さぁここまでで色は光の波長によりきまるということを知った。さらにこの話をここでは深めてみよう。少々難しい式も登場することになるが頑張ってみよう。
　ニクロム線に電気を通して発熱している様子を見たことがあるだろうか。今はLEDや蛍光灯などが多くなってあまり見られなくなったが白熱電球の光も発熱と共に発光していることが観察してみるとよくわかる。温度が高い物体は人間に見えるかどうかはともかくとして光を出しているのだ。

夏に日焼けするのは紫外線という光のせいでこの紫外線そのものは人の目に見えない。また、電気ストーブが暖かいのも赤外線が伝わってくるからでこの赤外線も人の目には見えない。

しかし、ここで不思議なことがある。太陽の下で日焼けした人はいるだろう。でもストーブで日焼けした人はいるだろうか。ストーブの火力をどんなに強くしても確かに太陽以上に暑くはなるけど日焼けしない。これはなぜだろうか。

１９世紀から２０世紀にかけて物理学会で非常に問題となった話題がこれと関係している。それは「黒体輻射」と呼ばれる問題だ。何も入っていないからの箱を用意しよう。それに小さなのぞき穴をあける。この箱の温度をどんどん上げていってのぞき穴から中の光を観察しようというのだ。

$Cell[GraphicsData[Metafile, CF5dJ6E]HGAYHf4PEfU^I6mgLb15CDHPAVmbKF5d0@0008m`0@0007@0002V0000 ... > {323.188, 144.938}, ImageMargins -> {{0., 0.}, {0., 0.}}, ImageRegion -> {{0., 1.}, {0., 1.}}]$

Figure 1

何も入っていないのだから真っ暗なままだろうと思ってはいけない。例えば鉄から刀を作るとき鉄を高温の中に入れると真っ赤になるのを見たことがあるだろう。同じように何もない箱の中は温度が高くなるとまず赤っぽくなってくる。箱は理想的で外界とのエネルギーのやりとりはすることなく内部の温度を自由に変化できるとしよう。のぞき窓も十分小さくエネルギーはほとんど漏れていかないとしよう。

【問題1】
さらに温度を上げ、のぞき窓から見ると今度は青白っぽくなり最後は白くなって再び見えなくなる。先に習った温度と波長の関係から考えてもこの理由はよくわからない。まるで温度が低い時は高い振動数の青側が死んでいて逆に温度が高くなると低い振動数側の赤が死んでいるようなことが起きているのである。色によるこの温度変化は遠い星の色にも同じようなことがいえる。赤く光る星より白く光る星の方が温度は高いのだ。さぁ君はこれをどう説明するか？

実はこの問題こそ新しい物理学の始まりとなったとても重要な問題なのだ。つまり既存の考え方ではどうしても説明がつかない。そこに大胆な発想が必要であったのである。しかし、ここではひるむことなくこの解答を探っていこう。その道のりは少々長いがそこには物理の重要な内容がぎっしり含まれている。数学的な難問には私たちにはMathematicaという高性能の武器があるので必要に応じて利用していこう。

さて、光の速さをｃ、光の振動数を ν、波長をλとすると次の関係が成り立つことを高校の物理で学習した。

(1)

さらに光は光子という小さな粒子からなると考えプランク定数をｈとして光子のエネルギーは次のように振動数に比例することも学習した。

(2)

この単純な２つの式はこれから理系の道を志す者とってはどこまでもついてくる非常に重要な式になる。
単純な式ほど物理的な内容はとても奥深い。しかし高校ではほとんどその奥深さには触れていない。だいたい定数ｈのとなりにあるνは振動数であって波の話しのところに登場したものだ。これと粒子と考えた光子がどう結びつくのか。これはそう簡単にはわからない。逆にこのイメージがつかめた人は文句なく物理学の最先端の道を志すべきであろう。問題１を解決するためにはこのイメージを少しだけ具体的にしていく。

式（１）は光の速さは波長×振動数であることを表している。波長は1回の振動で進む距離、そして振動数とは1秒間にどれだけ振動するかを表しているからこの式は光だけではなく波全てについて1秒間に進む距離を表している。光の場合重要なのはこのｃの値が次のような一定の値になることである。

(3)

この値は我々の知る限りの宇宙でどんな速度で自分が運動しているにも関わらず一定になる。これ以上速いものは宇宙で観測できるものとして存在しない。宇宙の構造に関係した極めて重要な定数である。同じようにプランク定数ｈも次のような定数である。このとても小さな数値も宇宙の様々な物理量の下限に関係した極めて重要な定数である。この２つの定数を土台に現代の物理は作られているともいえるだろう。

(4)

式（２）は最近信号機にもみられるLEDの光にも関係している。LEDの光は太陽や白熱灯とことなりその波長が一定だ。レーザーも一定の波長である。近くに最近解禁になった出力の弱いレーザーがあったらプリズムに通してみるといい。太陽の光のように何色もの光に分かれることはない。同じ色のままで屈折していく。

【問題2】
さらに色の異なったレーザーがあったらプリズムに通して比較するといい。赤と青とではどちらが大きく屈折するだろうか。この結果からなぜ空が青く、夕焼けは赤くなるかも説明がつくから自分でよく考えてみよう。

さて問題１を解決するにはまず光の出所を知る必要がある。LEDが等しく同じ色、すなわち同じ波長の光を出すという事実だけでもLEDがなぜ光るかという謎のヒントになる。光は原子の構造と関係しているのだ。式（１）と式（２）から同じ色の光は同じ振動数であり、エネルギーを持っている。同じ原子は同じ色の光を出すということは同じ原子の構造をもつものが多くあり、その構造には光を出したり、入れたりするしくみがあることになる。しかしも正確に決まったエネルギーが出入りしているのである。

ただ、人間の目はとても高感度で光子をとらえることができるが小さな粒子でもその中の原子の数はものすごく多い従って式(２)のエネルギーは大量の原子から出てくることになる。これが光の強さに関係している。しかしあくまで大量の光子が出ると振動数も大きくなることはないから注意しよう。原子とか光子とか電子とかを扱う場合教科書では１つの電子や光子を扱っても実際には大量の数が関係して現象は起きている。大量の粒子の平均を扱っているのかそれとも１個の粒子の特性を扱っているのかは物理を学ぶ時とても重要な注意点だ。例えばクラスの平均点を扱っているとき何点の人が何人くらいいるのかということはどうのように点数が分布しているかの分布関数が必要になる。ここでも同じように箱の中の光子がどれくらいのエネルギーを持っているものがどれくらいいるかを知るためにも分布関数が必要になるのだ。

原子の構造

【問題3】
ここまでに習った原子についての知識とある決まったエネルギーの光が原子に出入りしているということから原子の構造について考えてみよ。

【答】
原子が電子と原子核からなり、ちょうど太陽の周りを回る惑星のような関係であることを中学で習った。高校ではそう単純ではないことをさらに学習した。原子核の周りを本当に電子が周っているようなモデルでは電子が電気的な引力と釣り合って自分の軌道を維持しているとすると極めて高速な速さで運動していないといけないことになってしまうことを知った。実際の原子の構造を詳しく追求していくことはここではしない。LEDを光らせるには外から電圧を加えてあるエネルギーを与えてやれば一定の振動数の光が出る。しかもその後与えるエネルギーを増やしても光の振動数に変化はないのである。この事実で原子には次のような構造があることがわかる。

[Graphics:HTMLFiles/LecPic_81.gif]

Figure 2

原子核の周囲に電子があることは確かだ、原子核に比べて電子はとても小さいこともわかっている。それでいて１個の電子は電気的には１個の陽子と対等な電気量を持っている。でも１個の電子を見た人はいない。

さらに光はこの電子の軌道と関係している。それが図のように本当に円なのかどうかは今まだ触れない。でも少なくともいくつかの安定した軌道があって電子は安定した原子をつくり、さらにその原子は分子や物質を構成していく。しかし、様々な環境の変化で原子には外からエネルギーが出入りする。それを吸収したりするスポンジの役目が無かったら原子はすぐに壊れるか、まったく変化しない頑強なものとなるだろう。しかし現実にはそうならない。ということはそのしくみが必ずそこにあるということだ。

原子核は正の電荷を持った陽子と中性子から主に成り立っていることを学んだ。この原子核はとても固いと考えてよい。したがって原子の内部にエネルギーを貯めたり吐き出したりするクッションは電子が担っていることになる。原子の中におそらく複数の電子の軌道があり電子の軌道変化でエネルギーのクッション役をしていると考えるのである。

現実の物質は非常に多様な変化と種類がありその変化の主役も電子が担っているのである。生き物の体の中などで起こる化学変化はまさに一番外側の電子を色々な原子がやりとりすることだ。つまり電子は原子と原子が結合するボンド役もしていることになる。

このような現実をうまく説明するためにはエネルギーの違いによって原子核の周りにはいくつかの軌道がありそこに安定した電子があると考えたらいい。外側の軌道ほどエネルギーが大きいとしておけば最初電子をはエネルギーの低い軌道から入っていく。ちょうどその１つ外側の軌道にうつるだけのエネルギーが与えられれば電子はその軌道に移っていく。そしてその軌道から逆に落ちて１つ下の軌道に移る時にはそのエネルギー分を出すことになる。

[Graphics:HTMLFiles/LecPic_82.gif]

Figure 3

軌道の差のエネルギーが光子のエネルギーだとしたらどうだろう。みごとに同じ色の光が原子によって出てくる説明がつく。さらに上の図のようにおそらくそれぞれの軌道には最大に電子が入れる数が決まっていることになる。もし、一つに軌道にいくらでも電子が入れたらどんどん電子を１つの軌道につめこめばいいわけだから現実のような多様な原子の種類はできないだろうし、いくつもの軌道をつくる必要もなくなってしまう。

このようなエネルギーが異なった軌道がある考えをエネルギー準位という。そして各軌道に入れる電子の数ももう少し学習していくとそれは２個であることがわかる。以上によって下から順番に電子がつまっていく見事な構造ができて電子はその軌道を変化させる度に光子を出したり吸収したりするわけだ。

1個と多数を結ぶもの

原子から光子が出入りするしくみが少しわかった。箱の内部をつくっている物質も原子からできているから光子を出入りさせる。箱の内部は大量の原子で覆われているから一様な温度になった時にはおそらくその温度にもっともあったエネルギーを持った粒子が大量に出てくる。でもそれ以外のエネルギーをもった粒子も必ず出てくるだろう。温度というものを物理で扱う時は温度が全ての状態の平均を目安にした物理量であるということだ。したがってそこにはいくつかの情報は無視されていく効果が入っている。

ここでは光子1個と何もない真っ暗なブラックボックスの中の定常波を扱う。そこには光子は無数に様々な状態で存在していることが考えられる。とても以前に習った運動方程式みたいなものでは太刀打ちできない。そこでその橋渡しをする道具がいる。大量の粒子がある条件でどういう形になるか、こういうグラフを分布関数という。その関数を手探りで見つけようというわけだ。物理の分野では統計力学と呼ばれる専門分野がある。その一端がここで少し覗いてみよう。

肩慣らしにここで光子から離れてイメージのつかみやすい質量ｍの自由粒子に目をむけよう。この粒子がｎ個ある速さで運動しているとする。粒子の間の引力によるエネルギーが粒子の速さによるエネルギーより十分小さければまさにこれは気体のモデルで各気体分子が１つの粒子だと考え、これらはまったく自由な方向に運動していることになる。ただ、引力が働いてこのエネルギーが強くなると粒子は束縛され、先の原子核と電子のモデルのように全く自由には動けない。地球も太陽から離れて自由に動けないのは太陽と地球との間に強力な引力が働いているからだ。ここでは気体の分子のように自由に動いている粒子を考えることにしよう。

さて質量ｍ、速さｖで運動している自由粒子1個の粒子のもつエネルギーは次のようになった。

(5)

一方で高校物理の熱の所で習ったように温度Tのもとでは１つの自由度に等しく次のエネルギーが分配されるというエネルギー等分配の法則があった。

(6)

Ｔは絶対温度、kはボルツマン定数で次のような値をとる。

(7)

温度の単位はKで絶対温度を表すケルビンである。この数値を見てわかるようにとても小さくこれに次のアボガドロ数をかけてはじめて扱いやすい数値になる。この定数が1個と大量の数を結ぶ大きな意味を持つ。

(8)

自由度については最初の講座で少し触れた。次元とも関係した量であって１粒子の場合我々の空間はｘ、ｙ、ｚの３つの自由度がある。従ってエネルギー等分配の法則からは1個の粒子は温度Tのもとで次のエネルギーを得ることになる。

(9)

これからもたとえば単独の原子で気体になってるヘリウム（Ｈｅ）のような原子がどれくらいの速度で飛んでいるのか見積もることができる。Ｈｅの原子量は４であるだからアボガドロ数個だけあれば４ｇである。
したがって1個の質量は次のように求まる。

例えば温度がちょうど０℃であればＴは２７３Ｋであるから式(5),式(6)より

従ってヘリウム原子は音速よりはやく飛び回っていることになる。自分でも例えば水素分子について計算してみるといい。Ｈの原子量は１であるからは２の分子量を持つだだし、水素分子は次の図右のように原子の３つの自由度に加えて区別できる回転の２つの自由度が加わることに注意がいる。

[Graphics:HTMLFiles/LecPic_98.gif]

従って高校の授業で習ったように自由粒子(１個の自由度が３）がｎ個あれば全体の内部エネルギーUは次のように表すことができる。たったこれだけのことからあとは以前に習得した力積がわかっていれば気体分子がどんな方程式に従うかも導ける。ここでは寄り道なるので触れないが自分で挑戦してもいいだろう。

(10)

【課題１】
では本題に戻ろう。温度Tで平衡状態になっている時、エネルギーの状態にある粒子はどれくらいの数あるのか。これを表す分布を求めてみよ。

【答】
この解はインターネット等で調べるとほとんどは気体の位置エネルギーを考慮して理想気体の状態方程式を用いて算出しているのが多い。また、エントロピーの法則を利用して数式的に解くこともできる。しかし、ここでは数式をなるべく避けて原理的に考えてみることにする。まず自分の頭の中で先のエネルギー等分配の法則を思い出して考えを進めてみよう。与えられているのは1個のエネルギーの式のみだ。

そのためにはまず自由度（粒子が入ることができる器の数）を考えていかなくてはいけない。

一般にエネルギーが低い方安定であるからエネルギーが高い状態数はそんなにたくさんはないだろう。したがって状態数を表す分布はエネルギーが大きくなると逆に小さくなるような関数のはずだ。また、先のエネルギー等分配の法則は１つの自由度にｋTのエネルギーが分配されているのでエネルギーをこのｋTを１つの枠と考えこの枠で割ってやればその中の自由度の数になるとし、この数をSとしよう。

例えばSが６なら自由度の数は６つである。この自由度については全て同じエネルギーと考える。このように同じエネルギーの状態は複数存在することが現実に可能でこういう状態を縮退しているという。従って下の図は６つの状態が縮退していて同じエネルギーであるからこれを図のように便宜上6面体（サイコロ）で表現しよう。
もし、３つの状態が縮退していれば正３面体をイメージすればよい。ただこれはあくまでイメージをつかむためのモデルにしかすぎないことに注意しよう。

[Graphics:HTMLFiles/LecPic_103.gif]

例えばｋTの枠の中にいれるのが表裏の2つの自由度をもつコインが2個の場合の数は通りあり、もしコインではなくてABCの３つの自由度をもつ3面体が３個あればだけ場合の数はある。従って今エネルギーEの１粒子の自由度がSでその個数がｎの場合は場合の数wはとなる。この場合のsは次の式で表される。

(11)

このsは先にみたように単純な原子であれば３だから3次元の空間を占めていく。となるといいのだがそうではない。このsが何を表現しているかは次の節のエントロピーとエネルギーによる補足で考える。ここでは次のように簡単に考えてみる。

まず運動エネルギーEを持っている粒子が体積V、温度Tの中に１つある時を考えてみよう。たった１つの粒子だからきっと単純にいくと期待できる。温度が決まれば自動的に式(9)から運動エネルギーは決まり、自由度は３、従ってs=3と確定する。はずである。ところがそうはならない。常識的に考えてその理由はただ原子がｘ、ｙ、ｚの運動をしているだけでなく、例えば回転したり、振動したり、また何か箱の壁と相互作用したりするのではないかということが考えられる。

ところがである。そうしたことでも解決できない問題が箱のなかのたった1つの原子にはある。その解決はもはやこの原子が粒子として考えるのではなく光の時のように波になって定常波をつくっていると考えないとうまくいかない、そうすると粒子の密度が影響してきたりする。この時は全く新しい考え方を余儀なくされる。つまり厳密に考えていくと式(6)のエネルギー等分配の法則が成り立たないのだ。原則の１つを崩す事件がここに起きた。この事件続きは後にしてここでは式(11)を単純にまず書き改めよう。

(12)

基準の枠はｋTに改める。このsは温度Tが非常に大きな個数ｎから決まる値に対してsやEは非常に小さく正確に決まらないゆらぎをもった値になる。そこで高校の物理で微少変化量を表すΔをsとEにはつけた。

次に今考えている箱の中は温度Ｔで平衡にある。さらに箱の中のエネルギーは全体ではＵとし、総個数をＮとすればエネルギーについて次の条件が成り立つ。

(13)

したがって今仮にエネルギーＥを持つ粒子に注目するとそれ以外は次の図で示すようにＵ\:ff0dEのエネルギーの状態をとることができるわけだ。１つ粒子のエネルギーを決めてもその周囲はさらにいろいろな状態をとることが可能であることを考慮しないといけない。

[Graphics:HTMLFiles/LecPic_113.gif]

この周囲の状態の数を考えよう。次の図のようにU-Eの領域について粒子が０，１，２，３・・・の場合についてｋTの枠の中に入れていく。下の図ではΔsが６で6面体(立方体）をいれている。これはサイコロが入っていると考えればよくてたとえば1個の場合では６通り、2個の場合では６×６通りだけの場合の数がある。n個ならでこれを空白から初めて非常にたくさんのN-1個まで足し合わせていくわけだ。

[Graphics:HTMLFiles/LecPic_115.gif]

ところが粒子を並べるときにが区別できないと考えると上図のよう粒子数が2個だと状態数が２！、３個だとの状態数が３！・・・粒子数ｎが増えるに従って重複した状態数がｎ！になっていることがわかる。そこで自由度数を足し上げるためにはこのｎ！で割っておかなくてはいけない。以上から1個の粒子のEを決めた時の全場合の数Wとすると粒子０の空白を１通りと考えて

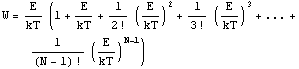W = E/kT (1 + E/kT + 1/2 ! (E/kT)^2 + 1/3 ! (E/kT)^3 +... + 1/(N - 1) ! (E/kT)^(N - 1))

(14)

となる。今Eのエネルギーを持つ粒子はだけの自由度をもっているから求める分布を確率で表すとエネルギーEを持つ粒子は温度Tの平衡状態ではこの確率をP(E)とするとこれは次の値に比例する。

(15)

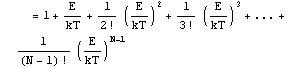= 1 + E/kT + 1/2 ! (E/kT)^2 + 1/3 ! (E/kT)^3 +... + 1/(N - 1) ! (E/kT)^(N - 1)

(15)

ここで指数関数の定義を思いだそう。

(16)

これを用いれば適当な定数をAとして式(15)は次のように書き換えることができる。

(17)

[Graphics:HTMLFiles/LecPic_125.gif]

$f[n_] := Sum[(-x)^i/i !, {i, 0, n}]$

[Graphics:HTMLFiles/LecPic_129.gif]

数式による補足（復習エントロピーとエネルギー）

式(12)が何を表現しているかもう少し考えてみよう。そのためには前回の熱とエントロピーの話を少し復習しよう。今温度Tは全体が平衡状態になっていてその時の温度であると考えるから系全体をから決まる広範囲な値である。これに対しEは粒子１つのエネルギーに相当し、非常に小さな局所的な値である。前回の講座でふれたように乱雑さを表すエントロピーsは状態数Wが大きくなれば大きくなり次のように定義されていた。

(18)

ところがもともとエネルギーはある状態の差として定義された。例えば簡単なコイン３個の系を考えてみよう。この系のエントロピーは次のように状態数Wを求めれば簡単に求まる。

(19)

この時、エネルギーとは例えば表の数から裏の数を引いた数というふうに約束できる。例えば次の図のように表が1個裏が2個の系Aと表が2個裏が1個の系Bではエネルギーは次のように計算される。

[Graphics:HTMLFiles/LecPic_134.gif]

Figure 4

一方でAの並べ方とBの並べ方をWA,WBとすると

(20)

となるからそれぞれのエントロピーは

(21)

となる。そこでこの２つの系を外界と断熱して接触させ平衡状態になったとすると。

(22)

となりエントロピーは系を混合させる前と後では後の方が増加しているというエントロピー増大の法則が確認できる。これに対しエネルギーは混合後のエネルギーをEとすると

(23)

となってエネルギー保存則が成立していることがわかる。さらにこのエネルギー０という状態は裏３個表3個の場合の並べ方だけ状態がある。さて何通りあるか自分で計算してみよう。他の場合にくらべエネルギー０はもっとも状態数が多いことがわかるだろう。

そこでエネルギーを決めるのには２つ状態の差を利用したから状態数としては２ついるということで式(11)は２で割り次のようにSを書きかえることにしよう。

(24)

さて簡単に復習してきたがもう一つ思い出そう。エネルギーEとエントロピーsは次の式で結ばれていた。

(25)

ここでΔは微積分の講座で紹介したように変化量を表し、非常に小さな変化の場合は次のように書きかえることもできた。

(26)

この式に式(12)をlogの微分に注意して代入すると

(27)

これから式(12)の意味は次のようになる。

(28)

エネルギーEの増分の効果がこれは全体の状態数に対しどれだけ状態数を増やすかという意味になる。
また、式(24)と式(14)から

(29)

ΔEの符号はEが大きくなれば状態数が減少する方向に選んで適当な定数をAとして求める分布関数は次のようになる。

(30)

箱の中の光子

それではいよいよ箱の中の光子に注目しよう。先にも注意したようにこの箱の中には大量の光子がはいっている。したがって温度を変化させていってもいくつものエネルギーを持った光子があって平均的には温度をあげれば全体のエネルギーは上がっていくだろう。光子は式(2)のようにエネルギーが振動数に比例している。ということはいくつもの振動数がこの箱の中にできて定常波を作っていることになる。

定常波については前回の講座でも触れた例えば弦の場合、長さLを固定すると次のように波長の異なったいくつかのモードの波ができる。

[Graphics:HTMLFiles/LecPic_150.gif]

光の速さｃは一定だったから式(1)から波長が小さいということは振動数が大きくエネルギーが大きいことになる。箱の中はこうした振動数の異なる定常波がいくつもできていることになる。さてこれと光子とどう関係しているのだろう。

$Plot[x^3Exp[-x], {x, 0, 10}]$

[Graphics:HTMLFiles/LecPic_156.gif]

プランクの公式を作成(MKS)

g = Plot[{U[c/(a λ), 1000], U[c/(a λ), 1200], U[c/(a λ), 1400], U[c/(a λ), 1600]}, {λ, 0, 10}, PlotRange->All]

[Graphics:HTMLFiles/LecPic_168.gif]

可視領域での温度別ふるまい

g = Plot[{U[c/(a λ), 3000], U[c/(a λ), 4000], U[c/(a λ), 5000], U[c/(a λ), 6000]}, {λ, 0, 1}, PlotRange->All]

[Graphics:HTMLFiles/LecPic_171.gif]

可視領域で足し合わせ。

$tc[t_] := Table[U[c/(a λ), t], {λ, 0.38, 0.78, 0.4/255}]$

最大値を求めて規格化

$tbc[t_] := Table[U[c/(a λ), t], {λ, 0.38, 0.78, 0.4/255}]/mx[t]$

[Graphics:HTMLFiles/LecPic_178.gif]

重みをかけて足し合わせ、規格化関数を以下で定義

$sc[t_] := Sum[U[c/(a λ), t], {λ, 0.38, 0.78, 0.4/255}]$

$cc[t_] := Sum[λ U[c/(a λ), t], {λ, 0.38, 0.78, 0.4/255}]/sc[t]$

次のように温度が高いと波長が短い方にずれる。

[Graphics:HTMLFiles/LecPic_190.gif]

３刺激値をかけて足し合わせ

cR[x] = Abs[fr[x]]/Max[fr[x], fg[x], fb[x], 0.00001] ; cG[x] = Abs[fg[x]]/Max[fr[x], fg[x], fb[x], 0.00001] ;

cB[x] = Abs[fb[x]]/Max[fr[x], fg[x], fb[x], 0.00001] ;

$sR[t_] := Sum[U[c/(a λ), t] Abs[fr[λ]]/Max[fr[λ], fg[λ], fb[λ], 0.00001], {λ, 0.38, 0.78, 0.4/255}] ;$

$sG[t_] := Sum[U[c/(a λ), t] Abs[fg[λ]]/Max[fr[λ], fg[λ], fb[λ], 0.00001], {λ, 0.38, 0.78, 0.4/255}] ;$

$sB[t_] := Sum[U[c/(a λ), t] Abs[fb[λ]]/Max[fr[λ], fg[λ], fb[λ], 0.00001], {λ, 0.38, 0.78, 0.4/255}] ;$

[Graphics:HTMLFiles/LecPic_201.gif]

$sR[t_] := Sum[U[c/(a λ), t] Abs[fr[λ]], {λ, 0.38, 0.78, 0.4/255}] ;$

$sG[t_] := Sum[U[c/(a λ), t] Abs[fg[λ]], {λ, 0.38, 0.78, 0.4/255}] ;$

$sB[t_] := Sum[U[c/(a λ), t] Abs[fb[λ]], {λ, 0.38, 0.78, 0.4/255}] ;$

$cc[t_] := Sum[λ U[c/(a λ), t] rgb[λ], {λ, 0.38, 0.78, 0.4/255}]/sc[t]$

[Graphics:HTMLFiles/LecPic_213.gif]

１０００ｋから７０００ｋまでの色チャート

TB = Table[{rgb[cc[1000 + 6000 i/255]], Rectangle[{i/255, 0}, {i/255 + 1/255, 1}]}, {i, 0, 255, 1}] ;

[Graphics:HTMLFiles/LecPic_220.gif]

次に放射強度を考慮する。
次のように強度は温度と共に上がる。

[Graphics:HTMLFiles/LecPic_222.gif]

赤の最大を6０００Ｋに設置

$RGB[t_] := Module[{max}, sR[t] = Sum[U[c/(a λ), t] Abs[fr[λ]]/Max[fr[λ], fg[λ], fb[λ], 0.0 ... ax>1, 1, sR[t]/max], If[sG[t]/max>1, 1, sG[t]/max], If[sB[t]/max>1, 1, sB[t]/max]] ]$

1000k～10000kまでの黒体輻射の色変化

TB = Table[{RGB[1000 + 9000 i/255], Rectangle[{i/255, 0}, {i/255 + 1/255, 1}]}, {i, 0, 255, 1}] ;

[Graphics:HTMLFiles/LecPic_229.gif]

明度を無視してＲＧＢの比のみ

Clear[Rec] ; Clear[red] ; Clear[sG] ; Clear[sB] ; Clear[sR] ;

$Rec[t_] := Module[{max}, sR[t] = Sum[U[c/(a λ), t] Abs[fr[λ]], {λ, 0.38, 0.78, 0.4/255}] ; ... ^-8], sG[t]/Max[sR[t], sG[t], sB[t], 1.*10^-8] , sB[t]/Max[sR[t], sG[t], sB[t], 1.*10^-8] ] ]$

1000k～10000kまでの黒体輻射の色変化
関数が全領域で定義されていないため紫はでない。

TB = Table[{Rec[1000 + 9000 i/255], Rectangle[{i/255, 0}, {i/255 + 1/255, 1}]}, {i, 0, 255, 1}] ;

[Graphics:HTMLFiles/LecPic_236.gif]

..........................................................................................................................
ガウス関数による近似で同じ処理をする。プログラムをカプセル化した。

$Rec[t_] := Module[{max}, Co[x_, w_, h_] := h Exp[-w (λ - x)^2] ; wb = 1000 ; wg = 400 ; ... sR[t]/max], If[sG[t]/max>gmax, gmax, sG[t]/max], If[sB[t]/max>bmax, bmax, sB[t]/max]] ]$

TB = Table[{Rec[1000 + 9000 i/255], Rectangle[{i/255, 0}, {i/255 + 1/255, 1}]}, {i, 0, 255, 1}] ;

[Graphics:HTMLFiles/LecPic_250.gif]

明度を無視してＲＧＢの比のみ

U[ν_, T_] := b (8 π h)/(c^3 (Exp[(h ν)/(k T)] - 1.)) (ν)^3

$Rec[t_] := Module[{min}, Co[x_, w_, h_] := h Exp[-w (λ - x)^2] ; wb = 1000 ; wg = 400 ; ... ], sB[t], min], sG[t]/Max[sR[t], sG[t], sB[t], min] , sB[t]/Max[sR[t], sG[t], sB[t], min] ] ]$

$General :: spell1 : スペル間違いの可能性があります．新規シンボル\"min\"はすでにあるシンボル\"Min\"に似ています．$

TB = Table[{Rec[1000 + 9000 i/255], Rectangle[{i/255, 0}, {i/255 + 1/255, 1}]}, {i, 0, 255, 1}] ;

[Graphics:HTMLFiles/LecPic_269.gif]

[Graphics:HTMLFiles/LecPic_274.gif]

３．画像処理

　さてここまで来たらいよいよ画像を取り込もう。次のようにしてファイルを取り込む。
PCで圧縮してない画像はBMPファイル形式だがその分容量が大きい。写真などのカラー画像はJPGファイルが主に用いられる。白黒や色の数が少ない場合はGIFファイルなどが用いられる。これらは画像圧縮の方法が異なる。
画像はなんでもいいですがあまり大きくないものを選びましょう。ファイル名はTest.jpgを適当な名称に変更してください。
Show[]コマンドで表示する。

　次のコマンドでMathematicaで扱うRGBのデータに変換します。

[Graphics:HTMLFiles/LecPic_291.gif]

左から赤、緑、青の順で３つがセットになってならんでいます。数値は８ビット表示で最小が０最小が２５５となります。
さてここから例えば赤のデータだけとり出すにはどうすればよいでしょうか。

{{255, 255, 255}, {255, 254, 255}, {252, 255, 255}, {255, 254, 253}, {255, 253, 255}, {254, ... 255, 255}, {254, 255, 253}, {252, 255, 255}, {255, 255, 255}, {255, 255, 253}, {255, 254, 255}}

Do[
tbR[j] = Table[Part[gp/256., j, i, 1], {i, 1, Xmax}] ;
tbG[j] = Table[Part[gp/256., j, i, 2], {i, 1, Xmax}] ;
tbB[j] = Table[Part[gp/256., j, i, 3], {i, 1, Xmax}] ;
, {j, 1, Ymax}]

tR = Flatten[Join[Table[tbR[j], {j, 1, Ymax}]]] ;

tG = Flatten[Join[Table[tbG[j], {j, 1, Ymax}]]] ;

tB = Flatten[Join[Table[tbB[j], {j, 1, Ymax}]]] ;

Clear[Splot] ; Clear[tb] ; Clear[tf] ; Clear[ts] ; Clear[SRplot] ;

$Splot[tb_List, dx_] := Module[{tf, ts, imax, num}, tf = Abs[Fourier[tb]] ; imax = Length[t ... 1) dx/imax, Part[tf, i]}, {i, 1, num}] ; ListPlot[ts, PlotJoined -> True, PlotRange -> All] ;]$

$SRplot[tb_List, dx_, xmin_, xmax_] := Module[{tf, ts, imax, ymax, num}, tf = Abs[Fourier[tb ... , i]}, {i, 1, num}] ; ListPlot[ts, PlotJoined -> True, PlotRange -> {{xmin, xmax}, {0, ymax}}] ;]$

[Graphics:HTMLFiles/LecPic_306.gif]

[Graphics:HTMLFiles/LecPic_307.gif]

[Graphics:HTMLFiles/LecPic_308.gif]

[Graphics:HTMLFiles/LecPic_310.gif]

{0.355469, 0.203125, 0.242188, 0.242188, 0.230469, 0.242188, 0.242188, 0.246094, 0.214844, 0 ... 57813, 0.277344, 0.269531, 0.273438, 0.265625, 0.257813, 0.234375, 0.234375, 0.210938, 0.355469}

[Graphics:HTMLFiles/LecPic_316.gif]

[Graphics:HTMLFiles/LecPic_318.gif]

[Graphics:HTMLFiles/LecPic_320.gif]

tRGB = Table[RGBColor[Part[tbR[j], i], Part[tbG[j], i], Part[tbB[j], i]], {i, 1, Xmax}, {j, 1, Ymax}] ;

[Graphics:HTMLFiles/LecPic_324.gif]

　次のようにすると白黒になります。

[Graphics:HTMLFiles/LecPic_326.gif]

[Graphics:HTMLFiles/LecPic_328.gif]

Figure 5

　次のようにマイナスをつけるとどうなるでしょうか。

[Graphics:HTMLFiles/LecPic_331.gif]

　次のようにすると青を３割にできます。ｒ、ｇ、ｂの値を変えてやってみましよう。

Show[Graphics[RasterArray[Apply[(RGBColor[
r * #1, g * #2, b * #3] &), gp/256., {2}]]]
, AspectRatio -> 1] ;

[Graphics:HTMLFiles/LecPic_340.gif]

　画像処理のソフトのように境界を強調するには次のようにする。

ListDensityPlot[ListConvolve[Ag, ListConvolve[Bg, gp[[All, All, 1]]/256.]], Mesh -> False] ;

[Graphics:HTMLFiles/LecPic_345.gif]

　では立体的に見えるこの画像を本当に立体化してしまおう。
次の２つのコマンドをShift+Enterで入力する。

Timing[igp = ListInterpolation[gp[[All, All, 1]], {{0, 1}, {0, 1}}, InterpolationOrder -> 1] ;] ;

Plot3D[igp[x, y], {x, 0, 1}, {y, 0, 1}, Mesh -> False, Axes -> False, Boxed -> False, PlotPoints -> 200]

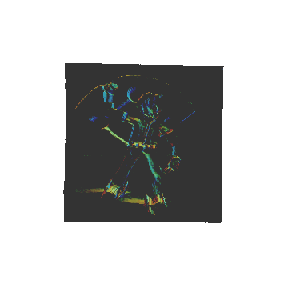
-SurfaceGraphics-

この画像はマウスで自由に回転できる。
さらに次のようにFigur１の画像の座標を見て画像を拡大して切り出す。切り出す時は｛ｙ座標｝、｛ｘ座標｝というふうに入れることに注意。

Take :: take : {{{53, 54, 58}, {32, 33, 38}, {38, 38, 46}, << 5 >>, {41, 41, 49}, {33, 34, 39}, << 20 >>}, << 9 >>, << 23 >>} の210から260の位置が取れません．詳細

[Graphics:HTMLFiles/LecPic_354.gif]

画像のサイズは小さくなった。でもこれではモザイクが入ってどうもみにくい。そこで実際に画像圧縮では次のような補完という技法が使われる。

........................................................................................
専門的には赤のチャンネル上で０と１の間で補完し、ｘ、ｙ座標に返す。
........................................................................................
次の2つのセルのプログラムをShift+Enterで入力

[Graphics:HTMLFiles/LecPic_358.gif]

まぁまぁモザイクがとれた感じになったね。

　参考文献

    ● Mathematicaの基礎    Mathematicaで何ができるか,主要なコマンドの解説
    　Mathmaticaの基礎    http://www.ne.jp/asahi/buturiwa/ai/educationM.htm
    　Mathematicaハンドブック　秀和システム    木村　広著　
           　Mathematica　数学の探索　トッパン　T・W・グレイ/J・グリン　著　時田　節/藤村　行俊訳　１９９４

    ● フ-リエ変換などの数学的基礎
        フーリエの冒険　　　ヒッポファミリークラブ　１９９４
        フーリエ解析　　　    岩波書店　　　福田礼次郎著　１９９７
        偏微分方程式    岩波書店    　及川正行著　　１９９７
        熱・波動と偏微分方程式　岩波書店　俣野　博/神保　道夫　著　2004

    ●　FFTやプログラム関係
        Cによる科学技術計算    CQ出版社        小池真一著

  ◎　Mathematica公式サイト:    http://www.wolfram.com
  *Mathematica と同じように数式処理できるソフトのＵＲＬ(高機能、高価)
   Ｍａｐｌｅ　 http://www.maplesoft.com/
   ＭａｔｈＣＡＤ　http://www.mathsoft.co.jp/

  *Mathematica と同じように数式処理できるソフトのＵＲＬ(無償版あり、安価)
  MuPAD http://www.mupad.de/
  Ｍａｘiｍａ　http://phe.phyas.aichi-edu.ac.jp/~cyamauch/maxima/
  Derive　http://education.ti.com/educationportal/　http://www.naoco.com/
  　（ＴＩ社日本代理店　関数電卓）


  著者のＨＰ　http://www.ne.jp/asahi/buturiwa/ai/educationM.htm

Created by Mathematica (July 8, 2007)