product.html

戻る　物理数学講座（Mathematicaシリーズ）

内積と外積

ベクトルの内積と外積の意味をMathematicaという数学ソフトを利用しながら理解してみよう。Mathematicaがなくてもコマンド部分はとばして視覚的に内積と外積のイメージをつかむとよい。
Mathematicaは現在のバージョンは６である。バージョン６は3次元図形の回転の操作が楽で描画も細かく色もつけることができる。
このノートはVer 6以下でも動くように作成されている。Ver6で動かすにはArrow[｛｝]の中の｛｝が余分に必要である。

内積の意味

次のような成分を持つx,y平面のベクトルAとBを考えよう.

In[1]:=

Mathematicaでは内積は次のようにピリオド．を使って演算する。

In[3]:=

Out[3]=

これが成分を用いて表示した内積の公式で、内積の結果は数値（スカラー）になることがわかる。
内積はベクトルのなす角をθ として次のようにも定義できた

(1)

もし、ベクトルｂが大きさ１の単位ベクトルならｂ＝１だから

となりこれはｂベクトル方向のスクリーンにaベクトルの影を映した影の長さに等しく、これを射影という。

この様子を見るために原点を含めて次のように再定義しよう。ClearコマンドはAという変数を初期化するという意味だ、以前に使われていなければ省略してよい。
Mathematicaはコマンドの終わりに;をつけるとそのコマンドの結果を画面に表示しない。
具体的に次のように原点Oを始点としてベクトルA（３，５）、ベクトルB（４，２）を作る。自分でも紙に描いてみよう。

In[1]:=

A,Bの単位ベクトルa,bを求めると次のようになる。単位ベクトルを求めるにはベクトルA、Bの大きさ（長さ）で割ってやればよい。
Mathematicaでは次のようになる。PartコマンドはAの成分のうちPart[A, 1]はｘ成分、Part[A, 2]はｙ成分を取り出すコマンドだ。

In[5]:=

Out[7]=

${3/34^(1/2), 5/34^(1/2)}$

Out[8]=

${2/5^(1/2), 1/5^(1/2)}$

矢印を描画するためのパッケージの読み込みを次のコマンドでおこなう。
パッケージの読み込みは１度おこなえばその後は終了するまで利用できる。(Ver6では必要ない）

In[9]:=

AベクトルとBベクトルを描画してみると。Mathematicaでは次のよにうにShowコマンドとGraphicsコマンドで図形を表現できる。
Hueは数字の０から１までで色の変化をつけるコマンドだ。

In[14]:=

Show[Graphics[{Hue[0.6],Arrow[o,A],
Hue[0], Arrow[o,B]}],AspectRatio→Automatic]

[Graphics:HTMLFiles/product_18.gif]

Out[14]=

AspectRatio→Automaticというオプションは縦横比を１にさせるためである。
次に単位ベクトルa.bを描画してみると。

In[15]:=

Show[Graphics[{Hue[0.6],Arrow[o,a],
Hue[0], Arrow[o,b]}],AspectRatio→Automatic]

[Graphics:HTMLFiles/product_20.gif]

Out[15]=

同じ長さ1に変化し、角度は変化していないのがわかる。

次に式(1)の結果をみるため
Aベクトルと単位ベクトルのbベクトルの内積を取る,(結果を簡単化し、ｋ１として表示させる）
Simplifyというコマンドは結果を簡単にしなさいという意味だ。

In[18]:=

Out[18]=

この結果だけかけて単位ベクトルｂを延長する。結果をｂ１というベクトルに代入しよう。

In[19]:=

Out[19]=

延長したb1ベクトル（赤）ともとのAベクトル（青）を図示し、さらに両方の頭の部分を緑の線で結ぶ。

In[21]:=

Show[Graphics[{Hue[0.6],Arrow[o,A],
Hue[0],Arrow[o,b1],Hue[0.3],Line[{A,b1}]}],AspectRatio→Automatic]

[Graphics:HTMLFiles/product_26.gif]

Out[21]=

確かに直角三角形ができている。つまり青いベクトルAはベクトルB方向の赤いベクトルｂ１に射影されている。
緑の線cと射影したｂ１ベクトルが直角に交わっているかを内積をとって確かめてみよう。
そのために緑のベクトルｃを次のようにAとｂ１の差で定義する。

In[26]:=

Out[27]=

ｃとｂ１との内積が０になった。つまり直交していることが確認できた。

外積の意味

さて、次に外積の話に移ろう。2次元のベクトルの外積を表現するにはまず3次元空間を用意する必要がある。
そこで3次元ｘ、ｙ、ｚ空間上のベクトルを次のように決めよう。

In[28]:=

Mathematicaでは外積は普通の×ではなく次のようにESCキー+cross+ESCキーで入力する。
すると次のように×記号が小さく表現される。AとBの外積は次のような結果になる。

In[31]:=

Out[31]=

内積と異なり、これは３つの成分を持っているからベクトルということになる。しかも各成分にマイナス（差）が出ている。これは回転と関係していることを意味している。

さて今はAとBは2次元の平面上のベクトルだから次のようにｘ、ｙ平面上のベクトルはｚ成分を０として定義しなおそう。

In[32]:=

これで再びESCキー+cross+ESCキーで外積を計算させてみよう。
するとなんと、結果はｘｙ平面ではなくｚ軸方向にのみ値が出てくるではないか！

In[26]:=

Out[26]=

Out[138]=

(2)

この結果からわかるようにｘ、ｙ平面上のベクトルが作る外積はｚ軸上に値を持つ。
これが物理の右ねじの法則と関係していて、モーメントや電磁力など様々な分野で登場する。
上の２つの結果は公式としても利用できる。自分で数値にして紙上で計算してみよう。
ｚ成分に現れるマイナスがうまく次の図のように回転を表していることが実感できる。
授業で地球コマを軸方向に回転させた時に感じた不思議な力を思いだそう。
自転車が回転すると安定するのも図のA×Bの方向の軸方向に慣性（いつまでも同じ状態にいようとする性質）が生じるからであった。
まさにこれは外積という数学が表現している。

[Graphics:HTMLFiles/product_42.gif]

Ver6　ではMathematica本体で簡単な図も描けるようになった。
また、ＡベクトルとＢベクトルのなす角θとして次のように大きさを定義することもできる。

(3)

改めて次のようにＡ，Ｂベクトルを定義し、図示してみよう。

In[37]:=

Mathematicaのバージョンが4以上６未満であれば次のように3次元回転のパッケージを読み込んでおくコマンドを実行する。
バージョン６以上であれば必要なくマウスでドラッグし、自由に始点を変えることができるし、色がつけられる。
ここでは残念ながらVer５まででも動作するようにしてあるので色はつかない。

In[35]:=

In[44]:=

Show[Graphics3D[{Line[{o,A}],
Hue[0], Line[{o,B}],Hue[0.8]}],AspectRatio→Automatic]

-Graphics3D-

Out[44]=

図をマウスで回転させてみよう。
どのように回転して見ても２つのベクトルが同一平面上にあることが確認できた。

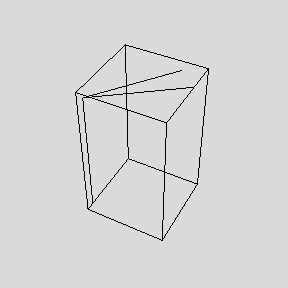
では次にさらに外積P=Ａ×Ｂを合わせて描画させる。

In[45]:=

P=A×B;
Show[Graphics3D[{Line[{o,A}],
Hue[0], Line[{o,B}],Hue[0.8], Line[{o,P}],Hue[0.6]}],AspectRatio→Automatic]

-Graphics3D-

Out[46]=

確かに外積はＡにもＢにも垂直になっていてＺ軸の高さとして向きがきまる。つまり外積Ａ×Ｂは
ＡからＢにむかう右ねじの向きを持つベクトル量である。

内積の時と同じように単位ベクトルになおして描画してみよう。

In[47]:=

Out[49]=

Out[50]=

Out[51]=

In[52]:=

Show[Graphics3D[{Line[{o, a}], Hue[0], Line[{o, b}], Hue[0.8], Line[{o, p}], Hue[0.6]}], AspectRatio -> Automatic]

-Graphics3D-

Out[52]=

次にa,bの単位ベクトルが次のように90°をなしていたらどうなるか図示してみよう。
その前に90°になったか内積と外積で確認する。

In[41]:=

$a = 1/2^(1/2) {1, 1, 0} ;$

$b = 1/2^(1/2) {1, -1, 0} ;$

Out[43]=

Out[44]=

内積が０外積はｚ成分が\:ff0d1となった。
つまり内積と外積の結果も90°で交わっていることがわかる。
では描画させてみよう。

In[45]:=

Show[Graphics3D[{Line[{o, a}], Hue[0], Line[{o, b}], Hue[0.8], Line[{o, p}], Hue[0.6]}], AspectRatio -> Automatic]

-Graphics3D-

Out[45]=

図のように視点が斜めであるが、全て長さが１になることがわかる。つまり、なす角が90°の時、外積は最大になる。
これは物理のモーメントでも力の向きと支点から作用点までの長さのベクトルが直角になっている時、最大になった。

外積の大きさ、この場合はＺ軸の高さは実はAベクトルとＢベクトルをそれぞれ平行移動してつくる平行四辺形の面積に一致している。

これを確かめるために次のような直交していない単位ベクトルＡ，Ｂと原点を再定義しよう。

In[26]:=

$A = 1/2^(1/2) {1, 1} ;$

これを描画し、さらにベクトルでつくられる平行四辺形を黄色でぬる。

In[63]:=

Show[Graphics[{Hue[.15], Polygon[{o, A, A + B, B}], Hue[0], Arrow[o, A], Hue[0.6], Arrow[o, B]}], AspectRatio -> Automatic]

[Graphics:HTMLFiles/product_78.gif]

Out[63]=

式１からこの２つのベクトルのなす角は次のように求めることができる。
ArcCos[θ]はＣｏｓの値がわかった時にθを求める関数である。三角関数表の逆引きと考えればよい。

In[64]:=

Out[64]=

角度の単位は２πを360°としたラジアンであることに注意する。πの１／４だから４５°の角度をなしていることがわかる。
図の平行四辺形の面積は高さが１×Cos ()だから＝
よって面積もになる。

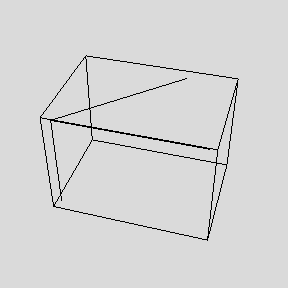
これは次のように改めて3次元空間で外積を定義し、3次元で見てみると平行四辺形の面積がちょうどｚ軸方向の高さが外積の大きさとして表現されていることがわかる。

In[46]:=

$A = 1/2^(1/2) {1, 1, 0} ;$

Out[50]=

${0, 0, -1/2^(1/2)}$

y軸とｘ軸の中間上にあるAからｘ軸上のBにまわすと向きはz軸の負の向き、つまり右ねじの進む向きに外積の向きが決まることがわかる。
その大きさが平行四辺形の面積に一致するのだ。この関係が物理学で大きな意味を持つ。

In[51]:=

Show[Graphics3D[{Hue[0.6], Line[{o, A}], Hue[0], Line[{o, B}], Hue[0.8], Line[{o, p}]}], AspectRatio -> Automatic]

-Graphics3D-

Out[51]=

内積はスカラーだからa.bもb.aも同じ値にあるしかし、外積の場合は次のようにa×ｂ＝\:ff0dｂ×aであることがわかる。
ねじを反対に回すと逆に進むことに対応する。

In[71]:=

Out[71]=

${0, 0, 1/2^(1/2)}$

これも図示して確かめてみよう。

In[72]:=

Show[Graphics3D[{Hue[0.6], Line[{o, A}], Hue[0], Line[{o, B}], Hue[0.8], Line[{o, p}]}], AspectRatio -> Automatic]

-Graphics3D-

Out[72]=

すでに行列を学習している場合は式２の第３成分は行列式に等しいことがわかる。
行列式も面積と関係しているのだ。
従って次のようにベクトルAとBから2次元の行列を再定義して行列式をとると

In[73]:=

$A = 1/2^(1/2) {1, 1} ;$

Out[77]//MatrixForm=

$(\[NoBreak] {{1/2^(1/2), 1/2^(1/2)}, {1, 0}} \[NoBreak])$

MatrixFormは行列表現にするコマンド、Detが行列式をとるコマンドである。

Out[78]=

みごとにＡ×Ｂの大きさに一致している。

残念ながら現教育課程の高校の数学では外積はほとんど語られることはない。しかし、高校で学ぶ物理学の中身と外積はとても重要で奥深い関係にある。
力学ではモーメントや惑星の運動つまり太陽の周りを回る地球などの惑星は実は完全な円ではなく楕円を描いている。
しかもその公転していく速さは実は一定ではない。一定なのは単位時間に軌道と太陽を結ぶ線がつくる面積なのだ。これを面積速度という。
面積速度が一定であることは万有引力の法則も導く。さらに電磁気の世界は外積で統一的に表現できる。
この講座で外積と内積について視覚的理解できればいまのところ大丈夫だ。

Created by Mathematica (August 20, 2007)