偏光板

　物理に戻る　　　　　【偏光と複屈折】偏光板の実験

＊対象:高校2年（３年）
      ＊予備知識ベクトル成分、行列　光の偏光、干渉・屈折　（＊複屈折）
      ＊準備　偏光板　３枚　セロハン数枚　ワークシート数枚　ＯＨＰ（演示の時）
      ＊補演習としてMathematicaの利用

＊本講座の前に本ＨＰの数学のコーナーにある「Ｍａｔｈｅｍａｔｉｃａによる２，３次元の探求を読んでおくのが望ましい。

使用した偏光板、自由に切ることができる。
図１

【導入】

偏光板を２枚用意して重ねて見てみよう。この時一枚目に対して、２枚目を回転させていくと何がおこるか。

図２図３

上の図のように９０度重ねるとほとんど向側は見えない。

また角度をずらすと見えてくる。さぁこれはなぜだろう。もっと不思議なことが３枚重ねるとおきる！？

さらに次のように無色透明のセロファンを偏光板の上に重ねる

図４図５

そして図５のようにもう一枚重ねると、きれいな色がつく、この色はセロファンの厚さや

重ねる角度によって異なる。偏光板を回転させると万華鏡のように色も変わる、さて

これはなぜか？！

【偏向の復習】

＊円偏光と直線偏光

前回のParamericPlot3Dを用いて偏光の様子を見てみよう。

次の命令文はｘ方向には4cos[a t] ｙ方向には4Sin[b t]、z方向にはtの値を持ってｔが０から４πまで

進んだグラフを表示させる。

例えばa=b=1であれば次の図のように上から見れば円のようになる。
これを円偏向という。

[Graphics:Images/Henkou_gr_2.gif]

次にa=1,b=0でグラフを描かせると次のようになる。
これは上から見ると直線になる。
これを直線偏光という。

[Graphics:Images/Henkou_gr_4.gif]

光が物質の中に入るとその物質によってaやbの値が異なるので多様な偏向の組み合わせができる。

[Graphics:Images/Henkou_gr_6.gif]

Ｍａｔｈｅｍａｔｉｃａがあったらいろいろパラメーターを変え試してみるとよい。
さて、今回は少し、発展して光が偏光板サングラスや雲母、液晶みたいな分子の配列が等方でない非等方性物質の中に入る時のことを見ていく。これは複屈折といって実験２で扱う。

普段は我々の眼には多様な偏向が無数にたくさん入っているのでほとんど偏向については気づかない。そこでサングラスなどに使われている偏光板の出番である。

実験1:　3枚重ねのほうが2枚重ねより明るくなることがありえる？

     導入：偏光板を２枚渡し、遊ばせる
    　　　　　　・相対的な角度により透明度に差が出ることを確認【１回転の間に何度明暗が入れ替わるか】

　　問１：明暗が変化することを図に描いてモデルを作ってください。【事前にワークシートを配布】
    　　　　　　・代表に説明させる
    　　　　　　・何枚でも詩s錯誤できるようにする。

　　問２：９０度で偏光板を重ねるとほとんど見えないですね。
　　　　　では間に４５度にしてもう一枚いれるとどうなるでしようか。【偏光板３枚目を配布】
    　　　　　　・モデルに沿って説明させる。
　
　　問３：３枚目が入ると明るくなることを説明できるモデルに変更してみてください。

図６

上の図をよーく見よう。２枚重なっているところより３枚重なっているところの方があかるいぞ。

これは偏光板が次の図のようにスリットのようになっていてそのスリットの目に沿った光しか通過させない

からだという説明ではおかしいことになる。さて何がおきているのだろう。

まず自分で考えてみよう。

これは次の偏光板が図のようなスリットのモデルではおかしいことになる。

モデル１

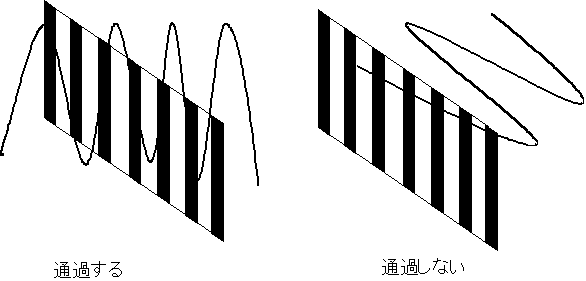
そこで次の図のように偏光板はＸ軸とＹ軸に分けたときＸ軸の成分を取り出す役目があるとしよう。

モデル２

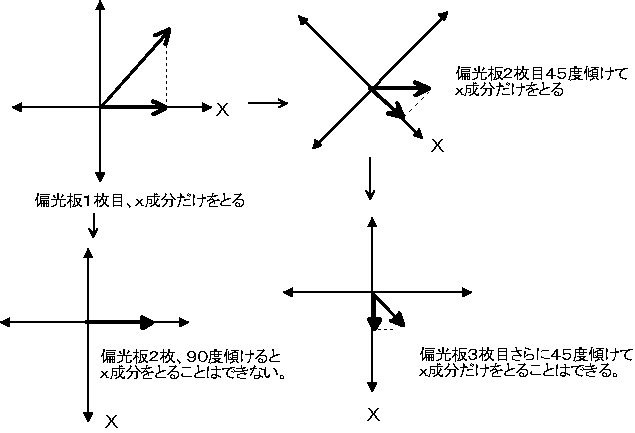すると９０度回転して２枚重ねるのでは光が通らなく暗くなる。でも途中に４５度回転したものがあると

少しだけど光を通すことになる。

つまり偏光板は座標軸の回転が関係していたわけだこの様子を次にＭａｔｈｅｍａｔｉｃａで詳しく見てみよう。

【簡単な説明】

光が１枚の偏光板を通過した後、次のような成分を持ったとしましょう。
(簡単のため振幅は１とします）

これはある方向のベクトルを１つ選んだことに相当します。【模範モデル１】
氓ﾌように回転の行列を決めましょう。
この行列は座標ｲを反時計回りにθだけ回転させます。

[Graphics:Images/Henkou_gr_8.gif]

この行列をH1に作用させると

このｘ成分とｙ成分のグラフをそれぞれ描いて見ると

[Graphics:Images/Henkou_gr_13.gif]

[Graphics:Images/Henkou_gr_14.gif]

つまり、ｘ成分とｙ成分は９０度ずれながら回転していくことがわかるね。
このグラフは振幅が正負に関係なく大きいところで明るく、０のところでほとんど真っ暗になることを表す。
氓ﾉ偏光板はｘ成分またはｙ成分のみ通過させるとしてそのための行列を次のようにおく。

[Graphics:Images/Henkou_gr_15.gif]

この行列は次のようにｘ、またはｙ成分だけを取り出すことができます。

[Graphics:Images/Henkou_gr_18.gif]

これで２枚目の偏光板Ｈの作用を次のように行列で表すことが可能になりました。

これがある角度θで１枚目の上に偏光板を置いたとき透過してくる光を表します。

（ただし、ここでは透過率は１としましょう）
簡単に言えば偏光板は偏光板に沿って座標ｲを設定し、そのｘ、またはＹ成分のみを取り出しているということなのです。

　　　【模範モデル１】

次に偏光板を９０度で２枚重ねたとき、通らなくなることを示してみよう。

φの値に関係なくｘ成分もｙ成分も０、すなわち真っ暗になるわけだね。
では２枚目を平行なときからはじめてぐるっと一周させた時の明るさはどうなるか、グラフにしてみよう。

[Graphics:Images/Henkou_gr_24.gif]

[Graphics:Images/Henkou_gr_27.gif]

これは実験とよくあっているね。しかもφは関係ないことが示されている。
では３枚目を４５度にして直角に重なっている２枚の偏光板にいれた時の式を求めてみよう。
これはまず２枚目を座標ｲをだけ回転し、さらに３枚目をそこからだけ回転させると考えて

[Graphics:Images/Henkou_gr_30.gif]

０でない成分が定数として出てきたね。【模範モデル３】
では真中の２枚目を平行なときからはじめてぐるっと一周させた時の明るさはどうなるか、先ほどのようにグラフにしてみよう。

[Graphics:Images/Henkou_gr_33.gif]

[Graphics:Images/Henkou_gr_35.gif]

振幅は２枚の時より小さくなっているね。
これも実験とよくあっているね。これで3枚重ねたときに明るくなる説明はついたわけだ。

実験２:　セロファンによる複屈折　透明なものに色がつく？

     導入：偏光板２枚の間にセロファンを入れ遊ばせる
　問１：
        ・セロハンを数枚重ねたらどうなるか【ついた色の関係】
        ・偏光板、セロファンを回転したらどうらるか
        ・２枚目の偏光板の働き

下の図は偏光板を奧に、セロファンを手前においたものである。

数字はセロファンを何枚重ねて貼ったかを表している。

これにもう一枚の偏光板を手前に重ねてみよう。

色がついてきたね。さらに偏光板を回転させる。

さらに平行になるまで回転すると

一回転の間に同じ色は何回現れるかためしてみよう。

では、なぜ透明のセロファンに色がついたのだろうか。

他のビニールではそうはいかないのはなぜか。

【簡単な説明】

[Graphics:Images/Henkou_gr_36.gif]

光が非等方性の物質(単ｲ結晶は基準モードが２つある)に入ると通常光の他に異常光ができる。この２嵭ﾞの光は90度偏光が偏っている。また物質中での両者の屈折率が異なる。このために物質を通過後その厚さに比例した位相差が生じ、２枚目の偏光板を通すことで２つの光は干渉し、ある波長の光が弱めあったり、強めあったりするために色がついて見える。

まずセロハンに入射する時の光の通常光を先のように表そう。１枚目のの偏光の向きとセロハンの光学軸方向との角度をφとおく。

通常光Hnと異常光Haはだけ偏光しているから先の回転させるＲを用いて

さらに、今度は波長が関係してくるから次のようなx方向進行波Sを通常、異常の場合について仮定しよう。
屈折率の違いはkn、kaの違いとして

[Graphics:Images/Henkou_gr_41.gif]

今、一枚のセロハンの厚さをｘとしよう。
従って一枚のセロハンのだけ通過したときは次のように表すことができる。

この光はまだ独立した偏光のため干渉しない。

偏光板の上にセロハンを載せて見ても色がつかないのはこのためだ。

では、もう一枚偏光板を９０度ずらして組み合わせよう。

通常なら光は通らないはずだ。

この時すでにφだけ回転していることに注意して

[Graphics:Images/Henkou_gr_45.gif]

あらら、通常光が０になっている。でもこれは実験ともあっていてセロハンの

最初の向きを１枚目の偏光板と同じにとったためだ。

では式を書き換えてセロハンも４５度回転させておいてあらためてやりなおして見よう。

[Graphics:Images/Henkou_gr_48.gif]

[Graphics:Images/Henkou_gr_49.gif]

２つの干渉可能な波が出てきた。

後は干渉の条件を考えればよい。ka xとkn xの差がこの時の位相差となる。

強弱の条件は自然数ｍについて

振動数をｆ通常光、異常光の速さをCn ,Ca 波長をラムダn ラムダａとすれば上式の強め合う条件は

Ca,Cnは物質に依存する。真空中のCoを１としてここでは仮に次のようにおく

ｍ＝１のとき

[Graphics:Images/Henkou_gr_55.gif]

これはちょうど紫色程度である。一般には今場合、波長は

[Graphics:Images/Henkou_gr_58.gif]

のように厚さｘに比例するからセロハンを2倍にするとこんどは赤色の光が観測できるはずである。
では次に偏光板は固定し、セロハンを回転させることを考えよう。
今、通常光と異常光の和は

であるがこの場合は先の結果から

[Graphics:Images/Henkou_gr_62.gif]

としてFの2乗が光の強度を表すとすると

[Graphics:Images/Henkou_gr_64.gif]

の形になっていることがわかる。

[Graphics:Images/Henkou_gr_67.gif]

これによってセロハンを１回転する間に強弱が2回くるからある色の波長が強めあったり弱めあったりが2回あるというこである。
つまり色では補色の関係が交互にくるわけだ。この様子をMathematicaに表現させてみよう。

[Graphics:Images/Henkou_gr_68.gif]

[Graphics:Images/Henkou_gr_69.gif]

[Graphics:Images/Henkou_gr_70.gif]

[Graphics:Images/Henkou_gr_71.gif]

これで今回のお話はひとまず終了である。

ここまできたら次の問題を考えてみよう。
【問題】
　　１．セロハンを直角に張り合わせるとかさなったところは何色にみえるか。
　　２．セロハンをまわした時に無色透明になるのはなぜか。
　　３．見る角度によって色が変化するのはなぜか。
　　４．セロハンを重ねていくと色はどう変わっていくか。

【応用ﾀ験】
　　・セロハンの厚さと屈折率をもとめる。
　　・セロハン（単ｲ結晶）以外に複屈折を示すものの観察。
　　・液晶のCRTの観察

参考文献等

「現代光科学　１，２」　大津　元一　朝倉書店
＊尚、本ファイルはMathematica Ver４を利用した。このファイルは次のサイトからダウンロード
、観閲可能　　　　　　　　　　　　http://www.ne.jp/asahi/buturiwa/ai/educationM.htm
また次のサイトも参考にするとよい。http://www-karc.crl.go.jp/opto/index-J.html
　　　　　　 2000.7.7　　柳瀬秀共

Converted by Mathematica July 8, 2000

物理に戻る 【偏光と複屈折】偏光板の実験

実験1: 3枚重ねのほうが2枚重ねより明るくなることがありえる？

実験２: セロファンによる複屈折 透明なものに色がつく？

参考文献等

　物理に戻る　　　　　【偏光と複屈折】偏光板の実験

実験1:　3枚重ねのほうが2枚重ねより明るくなることがありえる？

実験２:　セロファンによる複屈折　透明なものに色がつく？